A seismic trace represents a signal d(t) recorded
at a constant location x. The normal moveout operator
transforms a trace into a ``vertical propagation'' signal,
![]() , by stretching t into
, by stretching t into ![]() ().
For conventional PP seismic processing
the NMO transformation is generally described as a hyperbola.
For PS waves the traveltime moveout does not approximate a
hyperbola for large values of offset-to-depth ratio even for
an Earth's model consisting on horizontal layers embedded in a
constant P and S velocities.
().
For conventional PP seismic processing
the NMO transformation is generally described as a hyperbola.
For PS waves the traveltime moveout does not approximate a
hyperbola for large values of offset-to-depth ratio even for
an Earth's model consisting on horizontal layers embedded in a
constant P and S velocities.
One of the main characteristic of converted-wave data is their non-hyperbolic moveout in CMP gathers. However, for certain values of offset-to-depth ratio, it is possible to approximate the non-hyperbolic moveout in a CMP gather to a hyperbola ().
() developed a non-hyperbolic moveout equation
for converted-wave data. This equation consists on three
coefficients instead of the two coefficients for the hyperbolic
equation. Castle's non-hyperbolic moveout equation
is a function of both the P-velocity and the S-velocity.
Next, I present an expression for the
non-hyperbolic moveout equation in terms of ![]() .
.
Equation 1 is the third-order approximation for the total traveltime function of reflected PP or SS data presented by ():
| t2 = c1 + c2 x2 + c3 x4, | (1) |
| (2) |
For the second order approximation of the total traveltime function, () show that the first coefficient, c1, is simplified as
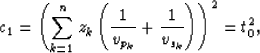 |
(3) |
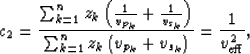 |
(4) |
The third coefficient, as presented by (), is
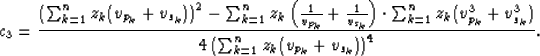 |
(5) |
![\begin{displaymath}
c_3 = \frac{z^2 \left [ (v_p+v_s)^2 - (\frac{1}{v_p} + \frac{1}{v_s})(v_p^3 + v_s^3) \right ]}{4 z^4 (v_p+v_s)^4},\end{displaymath}](img13.gif) |
(6) |
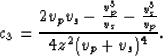 |
(7) |
| |
(8) |
|
nhterm
Figure 1 Non-hyperbolic term as a function of the offset-to-depth ratio. | 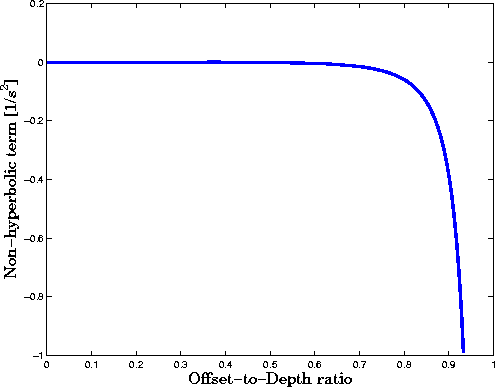 |
The coefficient c3 is the term in the total traveltime function that controls the non-hyperbolicity characteristic for PS reflections. Figure 1 plots equation 8, as a function of the offset-to-depth ratio. Notice that the non-hyperbolicity is primarily observed for large values of the offset-to-depth ratio, this conclusion validates the assumption of (), that is the non-hyperbolic moveout can be approximated with a hyperbola for small values of the offset-to-depth ratio. Also, note that the correction is always negative and ignoring it will result in overestimates values for the velocities.
Substituting equations 3, 4 and 8 into the total traveltime equation 1, I obtain the non-hyperbolic moveout equation for PS data
| |
(9) |
Figure 2 shows the traveltime computed with equation 9, with a constant P-velocity of 2 km/s, and S-velocity of 0.6 km/s, a maximum absolute offset of 7 km, and four horizontal reflectors at depths of 0.8, 1.5, 2.2, 2.9 km. The dotted curve represents non-hyperbolic moveout, equation (9), and the solid curve represents the hyperbolic moveout equation, that is omitting the third term in equation (9). Observe that for deeper reflectors and small offset both curves match reasonably well.
|
nhnmo
Figure 2 Non-hyperbolic traveltime comparison with the hyperbolic approximation. | 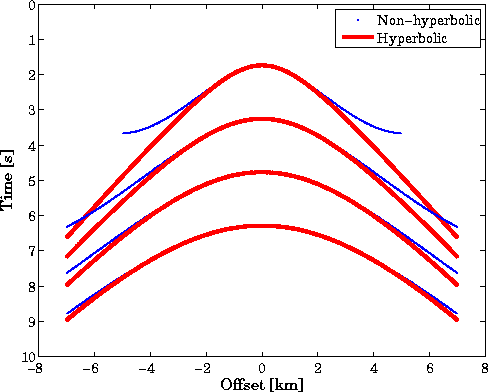 |