Next: Synthetic data test
Up: PS angle-domain common-image gathers
Previous: Mapping of PS-ADCIGs
I present a method to implement
equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
First, I describe the method and then illustrate it
with a simple synthetic example. Throughout
this section, I will refer to two different methods:
first, the conventional method, and second, the
proposed method. The conventional method
consists of the transformation from SODCIGs into ADCIGs
as in the single-mode case Sava and Fomel (2003).
Figure
.
First, I describe the method and then illustrate it
with a simple synthetic example. Throughout
this section, I will refer to two different methods:
first, the conventional method, and second, the
proposed method. The conventional method
consists of the transformation from SODCIGs into ADCIGs
as in the single-mode case Sava and Fomel (2003).
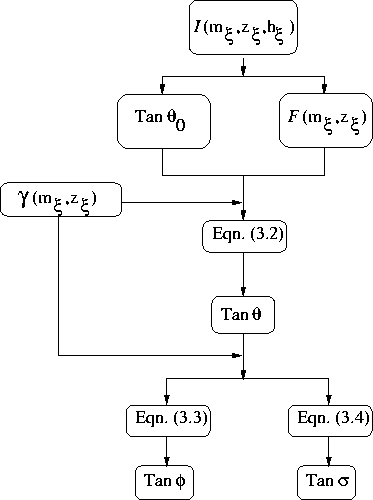
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the flow chart
for the proposed method.
presents the flow chart
for the proposed method.
flowADCIG
Figure 2 Flow chart to
transform the
subsurface-offset common-image gathers into the angle domain.
The flow diagram
also presents the mapping into P-ADCIGs
and S-ADCIGs.

The flow in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the basic
steps to implement and obtain the true angle-domain common-image
gathers for converted-wave data (PS-ADCIGs). First, I use
the final image,
presents the basic
steps to implement and obtain the true angle-domain common-image
gathers for converted-wave data (PS-ADCIGs). First, I use
the final image, 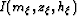 , to obtain two main pieces of information:
first, the pseudo-opening angle gathers,
, to obtain two main pieces of information:
first, the pseudo-opening angle gathers, 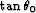 , using for example,
the Fourier-domain approach Sava and Fomel (2003); second,
the estimated image dip,
, using for example,
the Fourier-domain approach Sava and Fomel (2003); second,
the estimated image dip, 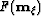 , using
plane-wave destructors Fomel (2002). For the second step, I
combine
, using
plane-wave destructors Fomel (2002). For the second step, I
combine 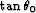 and
and 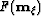 together with the
together with the
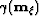 -field using equation
-field using equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to obtain true
converted-wave angle-domain common-image gathers.
Finally, I map these PS angle-domain common-image gathers into both
the P-ADCIGs and the S-ADCIGs through equations
to obtain true
converted-wave angle-domain common-image gathers.
Finally, I map these PS angle-domain common-image gathers into both
the P-ADCIGs and the S-ADCIGs through equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , respectively.
, respectively.
ps-all-new
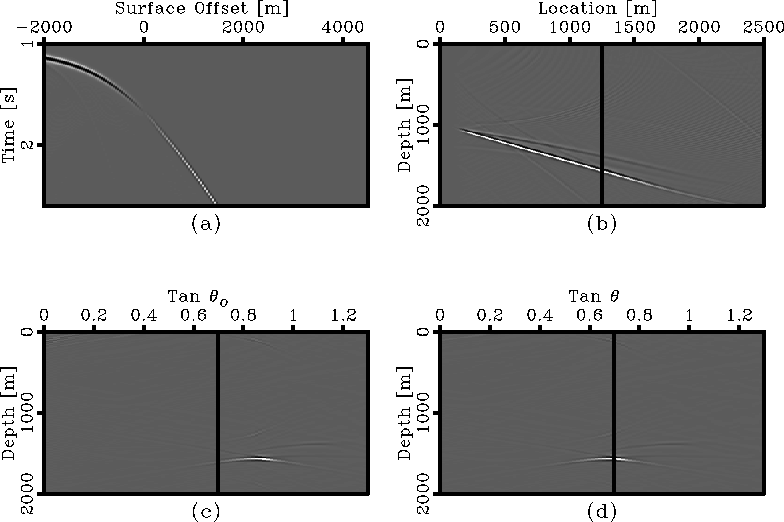
Figure 3 Synthetic
example that illustrates the method in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Panel (a) is a single shot
gather for a
. Panel (a) is a single shot
gather for a 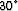 dipping layer event.
Panel (b) is the image of this single shot gather.
Panel (c) is the pseudo-opening angle,
dipping layer event.
Panel (b) is the image of this single shot gather.
Panel (c) is the pseudo-opening angle, 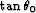 .Panel (d) is the true PS-ADCIG.
.Panel (d) is the true PS-ADCIG.





A simple synthetic example illustrates
the flow in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The synthetic dataset
consists of a single shot experiment over a
. The synthetic dataset
consists of a single shot experiment over a
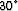 dipping layer. Panel (a) on Figure
dipping layer. Panel (a) on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the shot gather;
observe that the top of the hyperbola is not at
zero offset because of the reflector dip, and the polarity
flip does not happen at the top of the hyperbola.
Panel (b) shows the image of the single shot gather,
which represents
shows the shot gather;
observe that the top of the hyperbola is not at
zero offset because of the reflector dip, and the polarity
flip does not happen at the top of the hyperbola.
Panel (b) shows the image of the single shot gather,
which represents 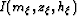 in the
flow chart of Figure
in the
flow chart of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The solid line in panel (b)
represents the location for the CIG in study.
. The solid line in panel (b)
represents the location for the CIG in study.
For this experiment the shot location is at
500 m, with the common image gather at
1000 m, and the geometry given for the
reflector, the half aperture angle
should be 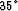 . This corresponds to
a value of
. This corresponds to
a value of 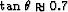 , that is
represented with a solid line on both common
image gathers at the bottom of Figure
, that is
represented with a solid line on both common
image gathers at the bottom of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The angle-domain common-image gather in panel (c)
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) was obtained
with the conventional method. Observe
that the angle obtained is not the correct one.
This ADCIG represents the tangent of the pseudo-opening angle,
was obtained
with the conventional method. Observe
that the angle obtained is not the correct one.
This ADCIG represents the tangent of the pseudo-opening angle, 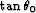 ,of flow
,of flow ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The ADCIG in panel (c) combined with the dip information,
.
The ADCIG in panel (c) combined with the dip information, 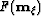 ,and the
,and the 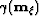 -field, results in the true
PS-ADCIG. Panel (d) presents the result of this process.
Notice the angle in the true PS-ADCIG coincides with the
correct angle.
-field, results in the true
PS-ADCIG. Panel (d) presents the result of this process.
Notice the angle in the true PS-ADCIG coincides with the
correct angle.
The last step for the flow chart in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) correspond to map the true PS-ADCIG into both a
P-ADCIG and an S-ADCIG, each one corresponding to the
P-incidence (
correspond to map the true PS-ADCIG into both a
P-ADCIG and an S-ADCIG, each one corresponding to the
P-incidence (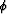 ) and S-reflection (
) and S-reflection ( ) angles,
respectively.
Figure
) angles,
respectively.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result for this transformation.
Panel (a) is the same image for the single shot gather on
a
shows the result for this transformation.
Panel (a) is the same image for the single shot gather on
a 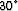 dipping layer. Panel (b) is
the corresponding true PS-ADCIG, which is
taken at the location marked in the image.
Panels (c) and (d) present the PS-ADCIG map into both the
P-ADCIG and the S-ADCIG, respectively.
Both angle gathers are obtained using
equations
dipping layer. Panel (b) is
the corresponding true PS-ADCIG, which is
taken at the location marked in the image.
Panels (c) and (d) present the PS-ADCIG map into both the
P-ADCIG and the S-ADCIG, respectively.
Both angle gathers are obtained using
equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) respectively.
respectively.
As in the previous experiment, the computed value for the
P-incidence angle is 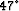 , which corresponds
to
, which corresponds
to 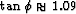 . The computed value
for the S-reflection angle is
. The computed value
for the S-reflection angle is 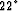 , which
corresponds to
, which
corresponds to 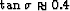 . Both of these values are
represented by the solid lines in each of the three
angle-domain common-image gathers on Figure
. Both of these values are
represented by the solid lines in each of the three
angle-domain common-image gathers on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
ps-ind-new
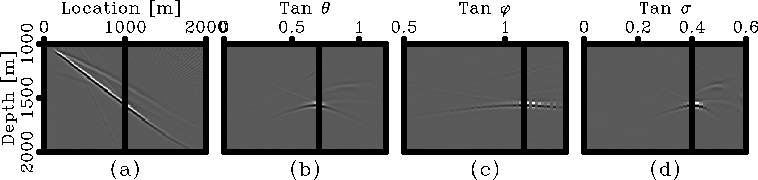
Figure 4 Synthetic example that
illustrates the last step of the method on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Panel (a) is the image of a single shot gather on a
.
Panel (a) is the image of a single shot gather on a 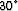 dipping
layer. Panel (b) is the true PS-ADCIG taken at the location of 1000 m.
Panels (c) and (d) are the P-and-S ADCIGs, respectively.
dipping
layer. Panel (b) is the true PS-ADCIG taken at the location of 1000 m.
Panels (c) and (d) are the P-and-S ADCIGs, respectively.










Next: Synthetic data test
Up: PS angle-domain common-image gathers
Previous: Mapping of PS-ADCIGs
Stanford Exploration Project
12/14/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
First, I describe the method and then illustrate it
with a simple synthetic example. Throughout
this section, I will refer to two different methods:
first, the conventional method, and second, the
proposed method. The conventional method
consists of the transformation from SODCIGs into ADCIGs
as in the single-mode case Sava and Fomel (2003).
Figure
.
First, I describe the method and then illustrate it
with a simple synthetic example. Throughout
this section, I will refer to two different methods:
first, the conventional method, and second, the
proposed method. The conventional method
consists of the transformation from SODCIGs into ADCIGs
as in the single-mode case Sava and Fomel (2003).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the flow chart
for the proposed method.
presents the flow chart
for the proposed method.