PS common-azimuth migration

The previous section describes the method we use to obtain a common-azimuth cube of PS data in a regular 4-D grid with dimensions ($t, {\rm cmp}_x, {\rm cmp}_y,h_x$). This common-azimuth cube is the input for the PS common-azimuth operator (PS-CAM). We present a review of the PS-CAM operator introduced by Rosales and Biondi (2005).

Point-scatterer geometry is a good starting point to discuss converted-wave prestack common-azimuth migration. The equation for the travel time is the sum of a downgoing travel path with P-velocity (v_p) and an upcoming travel path with S-velocity (v_s),

 

$$t=\frac{\sqrt{z^2+\Vert{\bf s} -{\bf x}\Vert^2}}{v_p}+\frac{\sqrt{z^2+\Vert{\bf g} -{\bf x}\Vert^2}}{v_s},$$ (6)

where $\bf s$ and $\bf g$ represent the source and receiver vector locations and $\bf x$ is the point-scatterer subsurface position.

Common-azimuth migration is a wavefield-based, downward-continuation algorithm. The algorithm is based on a recursive solution of the one-way wave equation Claerbout (1985). The basic continuation step used to compute the wavefield at depth $z+\Delta z$ from the wavefield at depth z can be expressed in the frequency-wavenumber domain as follows:

$$P_{z+\Delta z} \left (\omega,{\bf k_m},{\bf k_h} \right ) = ... ...} \left (\omega,{\bf k_m},{\bf k_h} \right ) e^{ik_z \Delta z}.$$ (7)

After each depth-propagation step, the propagated wavefield is equivalent to the data that would have been recorded if all sources and receivers were placed at the new depth level Schultz and Sherwood (1980). The wavefields are propagated with two different velocities, a P-velocity for the downgoing wavefield and an S-velocity for the upcoming wavefield. The basic downward continuation for converted waves is performed by applying the Double-Square-Root (DSR) equation:

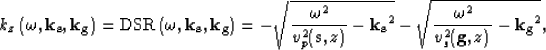$$k_z \left (\omega,{\bf k_s},{\bf k_g} \right )= \mbox {DSR} ... ... k_s}^2}- \sqrt{\frac{\omega^2}{v_s^2({\bf g},z)}-{\bf k_g}^2},$$ (8)

or in midpoint-offset coordinates,

 

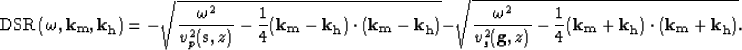$$\mbox {DSR} \left (\omega,{\bf k_m},{\bf k_h} \right )= -\sq... ...)}-\frac{1}{4}({\bf k_m}+{\bf k_h})\cdot({\bf k_m}+{\bf k_h})}.$$ (9)

The general continuation operator can then be expressed as follows Biondi and Palacharla (1996):

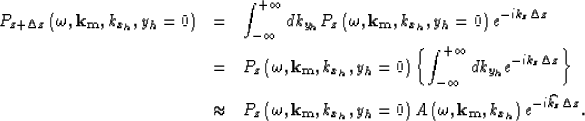$$\begin{eqnarray} P_{z+\Delta z} \left (\omega,{\bf k_m},k_{x_h},y_h=0 \right ) ... ...t (\omega,{\bf k_m},k_{x_h}\right ) e^{-i\widehat{k_z}\Delta z}.\end{eqnarray}$$ (10)

Since common-azimuth data is independent of k_yh, the integral can be pulled inside and analytically approximated by the stationary-phase method Bleinstein (1984). The application of the stationary-phase method is based on a high-frequency approximation. Rosales and Biondi (2005) present the stationary-path approximation for converted-wave data.

The expression for $\widehat{k_z}$ comes from substituting the stationary-path approximation into the expression for the full DSR equation (9):

$$\widehat{k_z}=\mbox {DSR} \left [\omega,{\bf k_m},k_{h_x},\widehat{k}_{h_y}(z),z \right ]$$ (11)

where

 

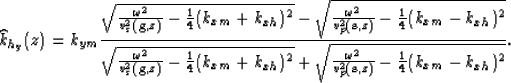$$\widehat{k}_{h_y}(z)=k_{ym}\frac{\sqrt{\frac{\omega^2}{v_s^2... ...ac{\omega^2}{v_p^2({\bf s},z)} -\frac{1}{4}(k_{xm}-k_{xh})^2}}.$$ (12)

The combination of the PS geometry regularization method and PS common-azimuth migration produces the final image from a converted-wave data set.