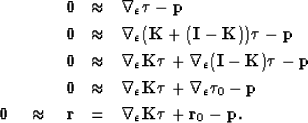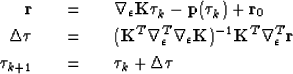Next: Preconditioning with the helical
Up: Lomask and Guitton: Flattening
Previous: Introduction
The flattening method described in Lomask et al. (2005) creates a time-shift (or depth-shift) field 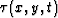 such that its gradient approximates the dip
such that its gradient approximates the dip 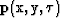 . The dip is a function of
. The dip is a function of  because for any given horizon, the appropriate dips to be summed are the dips along the horizon itself. Using the gradient operator (
because for any given horizon, the appropriate dips to be summed are the dips along the horizon itself. Using the gradient operator (![$\boldsymbol\nabla=[ \frac{\partial }{\partial x} \; \; \frac{\partial }{\partial y}]^T$](img4.gif) ) and the estimated dip (
) and the estimated dip (![${\bf p} = [{{\bf p}_x} \; \; {{\bf p}_y}]^T$](img5.gif) ), our regression is
), our regression is
| 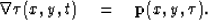 |
(1) |
To add regularization in the time direction, we apply a 3D gradient operator with a residual weight 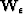 that controls the amount of vertical regularization defined as
that controls the amount of vertical regularization defined as
| ![\begin{displaymath}
{\bf W}_\epsilon\boldsymbol{\nabla}=
\left[
\begin{array}
{c...
... \ \frac{ \partial }{ \partial t} \end{array} \right] \quad ,\end{displaymath}](img8.gif) |
(2) |
where 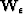 is a large block diagonal matrix consisting of two identity matrices
is a large block diagonal matrix consisting of two identity matrices 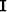 and a diagonal matrix
and a diagonal matrix  =
=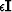 .For simplicity, we implicitly chain this weight operator to the gradient operator to create a new operator now defined as a 3D gradient with an weighting parameter
.For simplicity, we implicitly chain this weight operator to the gradient operator to create a new operator now defined as a 3D gradient with an weighting parameter  as
as
| ![\begin{displaymath}
\boldsymbol{\nabla}_\epsilon \quad = \quad \left[ \begin{arr...
...ilon \frac{ \partial }{ \partial t} \end{array} \right] \quad .\end{displaymath}](img13.gif) |
(3) |
The residual is defined as
| ![\begin{displaymath}
\bf r \quad = \quad { \boldsymbol{\nabla}_\epsilon \boldsymb...
...}{{\bf p}_x} \ {{\bf p}_y} \ {\bf 0} \end{array} \right] }.\end{displaymath}](img14.gif) |
(4) |
We solve this using a Gauss-Newton approach by iterating over equations (5)-(7), i.e.,
iterate {
| 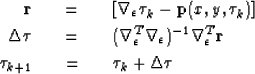 |
(5) |
| (6) |
| (7) |
} ,
where the subscript k denotes the iteration number.
We wish to add a model mask 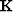 to prevent changes to specific areas of an initial
to prevent changes to specific areas of an initial 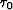 field. This initial
field. This initial 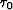 field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be a continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask we follow the same the development as the operator approach to missing data in Claerbout (1999) as
field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be a continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask we follow the same the development as the operator approach to missing data in Claerbout (1999) as
| 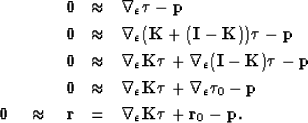 |
(8) |
| (9) |
| (10) |
| (11) |
| (12) |
Our resulting equations are now
iterate {
| 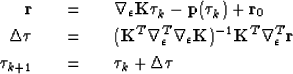 |
(13) |
| (14) |
| (15) |
} .
Typically, we solve equation (6) in the Fourier domain, however in equation (14), 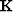 is non-stationary making its application in the Fourier domain difficult if not impossible. Therefore, for now we solve it in the time domain using conjugate gradients.
is non-stationary making its application in the Fourier domain difficult if not impossible. Therefore, for now we solve it in the time domain using conjugate gradients.
![]() that controls the amount of vertical regularization defined as
that controls the amount of vertical regularization defined as
![\begin{displaymath}
{\bf W}_\epsilon\boldsymbol{\nabla}=
\left[
\begin{array}
{c...
... \ \frac{ \partial }{ \partial t} \end{array} \right] \quad ,\end{displaymath}](img8.gif)
![\begin{displaymath}
\boldsymbol{\nabla}_\epsilon \quad = \quad \left[ \begin{arr...
...ilon \frac{ \partial }{ \partial t} \end{array} \right] \quad .\end{displaymath}](img13.gif)
![\begin{displaymath}
\bf r \quad = \quad { \boldsymbol{\nabla}_\epsilon \boldsymb...
...}{{\bf p}_x} \ {{\bf p}_y} \ {\bf 0} \end{array} \right] }.\end{displaymath}](img14.gif)
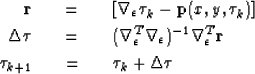
![]() to prevent changes to specific areas of an initial
to prevent changes to specific areas of an initial ![]() field. This initial
field. This initial ![]() field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be a continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask we follow the same the development as the operator approach to missing data in Claerbout (1999) as
field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be a continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask we follow the same the development as the operator approach to missing data in Claerbout (1999) as