




Next: Comparison of Radon Transforms
Up: Alvarez: Multiple attenuation
Previous: Introduction
The residual moveout of primaries in ADCIGs, under the approximation of
stationarity of the rays (local constant velocity) is given by Biondi and Symes (2004):
| 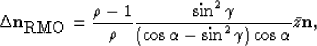 |
(1) |
where 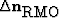 is the residual moveout function with
respect to the aperture angle
is the residual moveout function with
respect to the aperture angle 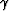 ,
, 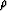 is the ration between the
migration and the true slowness,
is the ration between the
migration and the true slowness,  is the reflector dip,
is the reflector dip, 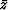 is
the true (unknown) depth of the reflector and
is
the true (unknown) depth of the reflector and 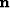 is the unit normal
vector to the reflector in the direction of decreasing depth. For a flat
reflector (
is the unit normal
vector to the reflector in the direction of decreasing depth. For a flat
reflector (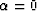 ) equation 1 reduces to
) equation 1 reduces to
| 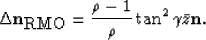 |
(2) |
For primaries, we can estimate the true depth 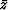 using the migration
depth at normal incidence z0 Biondi and Symes (2004) as
using the migration
depth at normal incidence z0 Biondi and Symes (2004) as
| 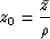 |
(3) |
which leads to the simple result
| 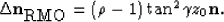 |
(4) |
For specularly-reflected multiples, Alvarez 2005
showed that,
for a flat reflector, the functional dependence between the image depth and the
aperture angle is given by
| ![\begin{displaymath}
z_{\xi_\gamma}=\frac{z_{\xi_\gamma}(0)}{1+\rho)}\left[1+\fra...
...^2-(1-\rho^2)\tan^2\gamma)}{\sqrt{\rho^2-\sin^2\gamma}}\right],\end{displaymath}](img12.gif) |
(5) |
where 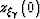 is the normal-incidence migrated-depth,
(i.e. z0) in the previous equations. There is an important and unfortunate
difference in notation, however, because
is the normal-incidence migrated-depth,
(i.e. z0) in the previous equations. There is an important and unfortunate
difference in notation, however, because 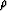 in equations 1
through 4 is the ratio of the migration to the true slowness
whereas
in equations 1
through 4 is the ratio of the migration to the true slowness
whereas 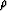 in equation 5 is the ratio of the migration to the true
velocity. Therefore, in order to get a better idea of how the approximation
for the RMO of the multiples (accounting for ray bending at the reflector
interface) relates to that of the primaries (neglecting ray bending), I rewrite
equation 5 replacing
in equation 5 is the ratio of the migration to the true
velocity. Therefore, in order to get a better idea of how the approximation
for the RMO of the multiples (accounting for ray bending at the reflector
interface) relates to that of the primaries (neglecting ray bending), I rewrite
equation 5 replacing 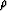 by
by 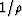 and
and 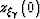 with
z0 to get:
with
z0 to get:
| ![\begin{displaymath}
z_{\xi_\gamma}=\left[1+\frac{\cos\gamma(\rho^2-(\rho^2-1)\tan^2\gamma)}{\sqrt{1-\rho^2\sin^2\gamma}}\right]\frac{z_0}{1+\rho}.\end{displaymath}](img15.gif) |
(6) |
Finally, since 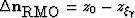 we get:
we get:
| ![\begin{displaymath}
\Delta \mathbf{n}_{\mbox{RMO}}=\left[1-\frac{\cos\gamma(1-(\...
...sqrt{1-\rho^2\sin^2\gamma}}\right]\frac{z_0}{1+\rho}\mathbf{n},\end{displaymath}](img17.gif) |
(7) |
which, for small 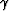 , reduces to
, reduces to
| 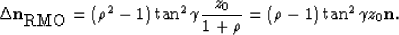 |
(8) |
This is the same as equation 4. This result is intuitively appealing
because it shows that the approximation of neglecting the ray bending at the
reflecting interface deteriorates as the aperture angle increases which is
when the ray bending is larger.
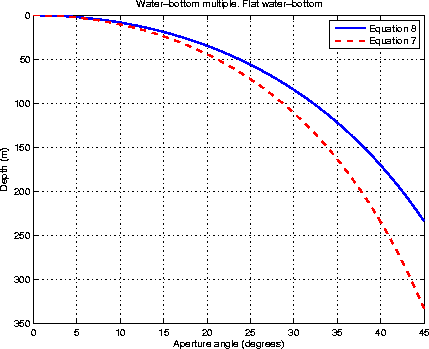
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison of
the residual moveout curves for an ADCIG computed with equations 7
(ray-bendinga pproximation) and 8 (straight-ray approximation).
The residual moveouts correspond to a water-bottom multiple from the flat
interface of a
two layer model where the top layer is water and the second layer is a half
space. The velocity of the water layer is 1500 m/s and its thickness is 500 m.
The velocity of the half space is 2500 m/s. The migration was done with the
true velocity model. Therefore, there is significant ray bending of the multiple
at the reflecting interface. Figure
shows a comparison of
the residual moveout curves for an ADCIG computed with equations 7
(ray-bendinga pproximation) and 8 (straight-ray approximation).
The residual moveouts correspond to a water-bottom multiple from the flat
interface of a
two layer model where the top layer is water and the second layer is a half
space. The velocity of the water layer is 1500 m/s and its thickness is 500 m.
The velocity of the half space is 2500 m/s. The migration was done with the
true velocity model. Therefore, there is significant ray bending of the multiple
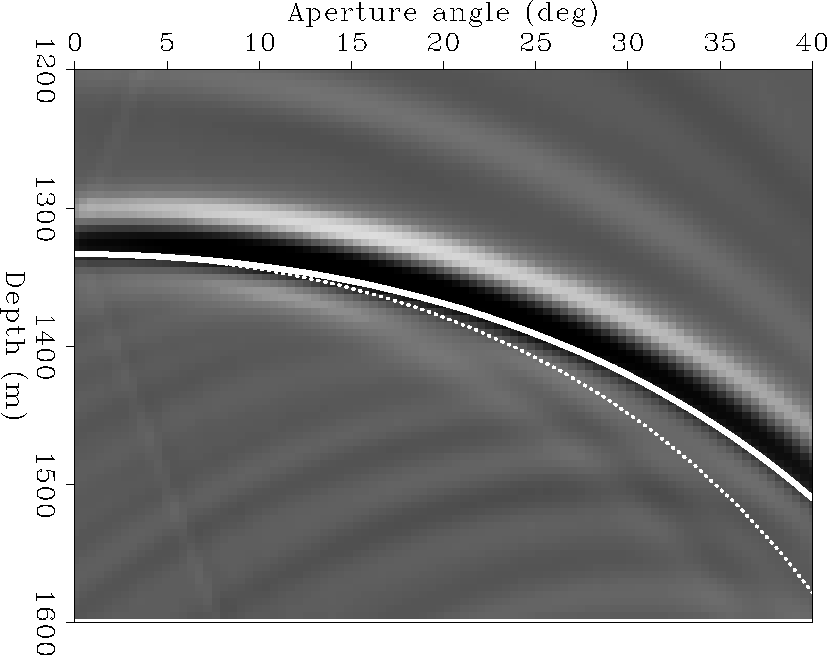
at the reflecting interface. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the actual ADCIG
with the depth moveout as a function of angle superimposed for both
approximations. For large aperture angles the departure of the straight ray
approximation can be significant.
shows the actual ADCIG
with the depth moveout as a function of angle superimposed for both
approximations. For large aperture angles the departure of the straight ray
approximation can be significant.
rmos2
Figure 1 Residual moveout curves for an ADCIG from a two
flat-layer model. The curves correspond to straight ray and the ray-bending
approximations to a water-bottom multiple.
|
|  |





adcig1
Figure 2 ADCIG for a water-bottom multiple from a two
flat-layer model. The dotted curve corresponds to the straight ray approximation
whereas the solid curve corresponds to the ray-bending approximation.
|
|  |










Next: Comparison of Radon Transforms
Up: Alvarez: Multiple attenuation
Previous: Introduction
Stanford Exploration Project
4/5/2006
![\begin{displaymath}
z_{\xi_\gamma}=\frac{z_{\xi_\gamma}(0)}{1+\rho)}\left[1+\fra...
...^2-(1-\rho^2)\tan^2\gamma)}{\sqrt{\rho^2-\sin^2\gamma}}\right],\end{displaymath}](img12.gif)
![\begin{displaymath}
z_{\xi_\gamma}=\left[1+\frac{\cos\gamma(\rho^2-(\rho^2-1)\tan^2\gamma)}{\sqrt{1-\rho^2\sin^2\gamma}}\right]\frac{z_0}{1+\rho}.\end{displaymath}](img15.gif)
![\begin{displaymath}
\Delta \mathbf{n}_{\mbox{RMO}}=\left[1-\frac{\cos\gamma(1-(\...
...sqrt{1-\rho^2\sin^2\gamma}}\right]\frac{z_0}{1+\rho}\mathbf{n},\end{displaymath}](img17.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison of
the residual moveout curves for an ADCIG computed with equations 7
(ray-bendinga pproximation) and 8 (straight-ray approximation).
The residual moveouts correspond to a water-bottom multiple from the flat
interface of a
two layer model where the top layer is water and the second layer is a half
space. The velocity of the water layer is 1500 m/s and its thickness is 500 m.
The velocity of the half space is 2500 m/s. The migration was done with the
true velocity model. Therefore, there is significant ray bending of the multiple
at the reflecting interface. Figure
shows a comparison of
the residual moveout curves for an ADCIG computed with equations 7
(ray-bendinga pproximation) and 8 (straight-ray approximation).
The residual moveouts correspond to a water-bottom multiple from the flat
interface of a
two layer model where the top layer is water and the second layer is a half
space. The velocity of the water layer is 1500 m/s and its thickness is 500 m.
The velocity of the half space is 2500 m/s. The migration was done with the
true velocity model. Therefore, there is significant ray bending of the multiple
at the reflecting interface. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the actual ADCIG
with the depth moveout as a function of angle superimposed for both
approximations. For large aperture angles the departure of the straight ray
approximation can be significant.
shows the actual ADCIG
with the depth moveout as a function of angle superimposed for both
approximations. For large aperture angles the departure of the straight ray
approximation can be significant.

