![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
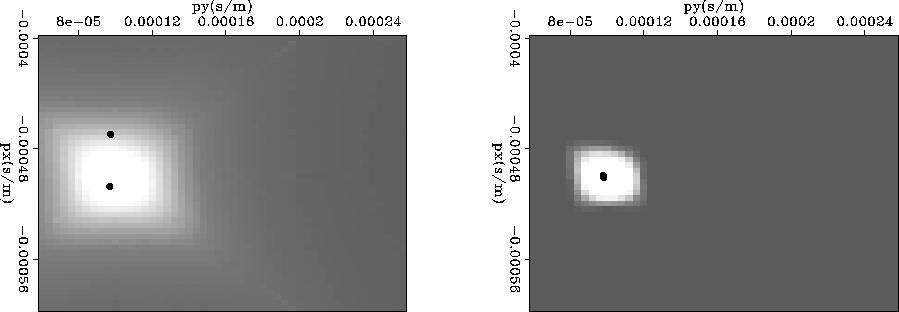
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows results when supplying LA with
model spaces produced by adjoint plane-wave decomposition verses
40 iterations of inversion with a single synthetic planewave used as
data. LA, told to choose at most 10, returned two picks for both
models despite only a single planewave existing in the data. LA will
not return one pick if the data supplied is not perfectly single
valued. In this example the data supplied to LA are coordinates with
energy in the figure times the duration of the wavelet in/out of the
plane. This leads to 3449 coordinate triples, some 500 being unique
since the quantization of the amplitudes used 10 levels.
shows results when supplying LA with
model spaces produced by adjoint plane-wave decomposition verses
40 iterations of inversion with a single synthetic planewave used as
data. LA, told to choose at most 10, returned two picks for both
models despite only a single planewave existing in the data. LA will
not return one pick if the data supplied is not perfectly single
valued. In this example the data supplied to LA are coordinates with
energy in the figure times the duration of the wavelet in/out of the
plane. This leads to 3449 coordinate triples, some 500 being unique
since the quantization of the amplitudes used 10 levels.
The adjoint model space has a diffuse character and diagonal streaks
away from main blob of energy (due to limited rectangular surface
acquisition). The model space was parameterized so that the energy
would not be symmetrically located on the px,py-plane. To balance
the distribution of energy, LA selected two points for the adjoint
model space that an interpreter would recognize as inappropriate.
After the inversion has clipped most of the acquisition tails and
moved the edge of the distribution away from the boundary of the
domain, the two picks returned are identical ![]() .
. ![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
 |
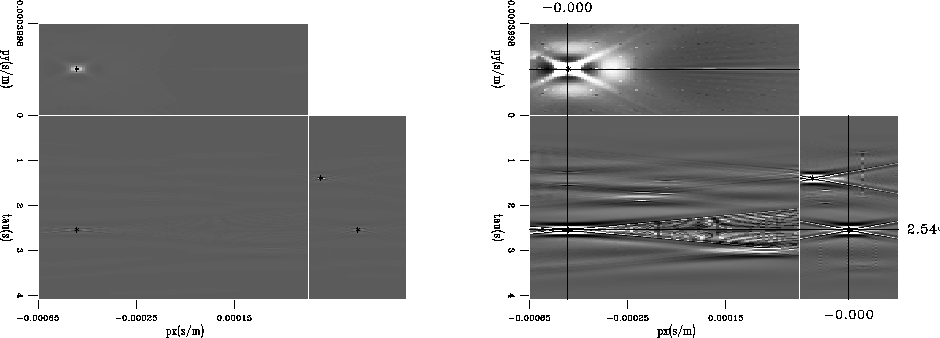
Six planewaves were modeled in a regular 3D acquisition geometry as data. The
data were inverted with the linear Radon transform. The inversion was stopped
after 1, 20, and 80 iterations. These data were then supplied to the modified
LA. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows inversion results after 20
iterations. The two panels show versions clipped
for display at 99 and 100% of the maximum value. Three picks from LA
are also plotted. The picks exactly overlay the maximum amplitude of
the energy. LA was initialized to select 10 coordinate triples. Only
six picks were returned. Note, however, that the lower right
coordinates are actually two picks very close together. One planewave
from the data space has not been picked. One of the planewaves had a
ray parameter px,py=(0.0005,0.0001) s/m, while the range of px
used for the inversion extended to only
px,py=(0.00045,0.0003) s/m. This plane thus falls outside of the model space
on the 2-axis, and the inversion is
not able to focuse the energy. Unfortunately, LA does not
recognize its significance either, and places an extra pick
semi-randomly close to another well established pick.
shows inversion results after 20
iterations. The two panels show versions clipped
for display at 99 and 100% of the maximum value. Three picks from LA
are also plotted. The picks exactly overlay the maximum amplitude of
the energy. LA was initialized to select 10 coordinate triples. Only
six picks were returned. Note, however, that the lower right
coordinates are actually two picks very close together. One planewave
from the data space has not been picked. One of the planewaves had a
ray parameter px,py=(0.0005,0.0001) s/m, while the range of px
used for the inversion extended to only
px,py=(0.00045,0.0003) s/m. This plane thus falls outside of the model space
on the 2-axis, and the inversion is
not able to focuse the energy. Unfortunately, LA does not
recognize its significance either, and places an extra pick
semi-randomly close to another well established pick.
 |
The approach seems robust for noisy data as well.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a section of the model space where
a uniform distribution of noise was added to the data space with the
picks selected from it by LA overlain. The picks are identical to the
previous runs when the variance of the added noise is
less than 0.001. The threshold value used was 1% of the maximum
value in the data. By increasing to higher levels (approximately
50%), the algorithm remains stable to variance values another order
higher. When the level of noise is too high so that the
thresholding of the data is not robust, the LA picks constantly
distribute themselves roughly evenly along the one-axis and about
centered across higher dimensions.
shows a section of the model space where
a uniform distribution of noise was added to the data space with the
picks selected from it by LA overlain. The picks are identical to the
previous runs when the variance of the added noise is
less than 0.001. The threshold value used was 1% of the maximum
value in the data. By increasing to higher levels (approximately
50%), the algorithm remains stable to variance values another order
higher. When the level of noise is too high so that the
thresholding of the data is not robust, the LA picks constantly
distribute themselves roughly evenly along the one-axis and about
centered across higher dimensions.
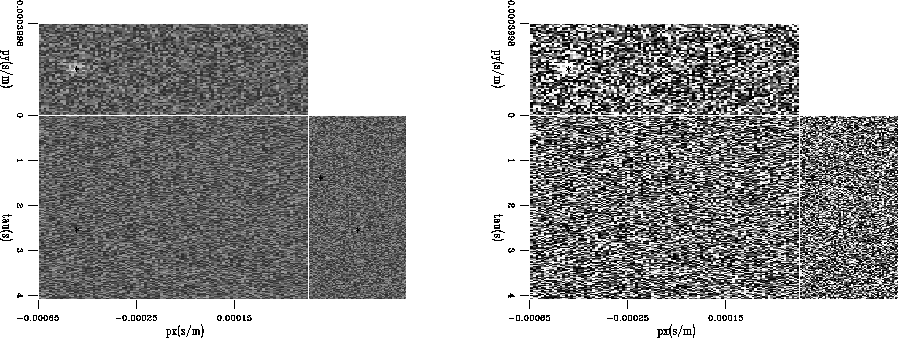 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Threshold for LA was 1% of the maximum
value in the input. Output picks are still reliable at this level.
. Threshold for LA was 1% of the maximum
value in the input. Output picks are still reliable at this level.