| |
(34) |
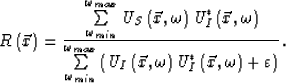 |
(35) |
|
Imaging_fig
Figure 2 The geometry explication of the cross-correlation imaging condition. S* is a virtual source of the real source S. The propagator L* is the conjugate of the downward propagator L. Therefore, both the propagator LH and L* collapse the wavefronts into a point--the imaging point P. | 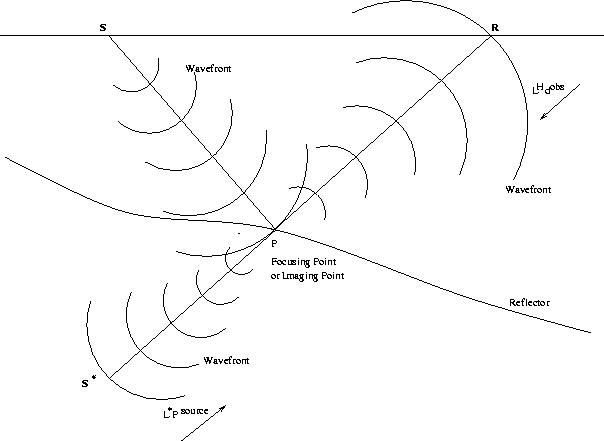 |
In the frequency domain, the extrapolated upcoming wavefield at the scattering point is
| |
(36) |
| |
(37) |
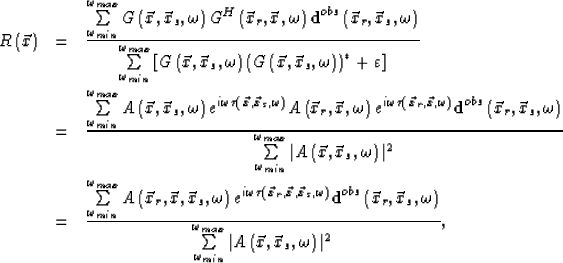 |
||
| (38) |