To calculate the Fourier transform of the reflection response of the
subsurface, ![]() , Wapenaar et al. (2004), proves
, Wapenaar et al. (2004), proves
| |
(1) |
Equation 1 dictates that the correlations of transmission wavefields must only be from individual transmission wavefields recorded over an interval, t, during which a single source is actively probing the subsurface. In this case, the zero-time of the correlations are correctly shared by the output of each correlation operation since each result is zero-phase. If more than one source function is active during a time window, or it is impractical to window the raw data around individual sources, the result of correlating the raw data will not yield the reflection wavefield R.
In practice, raw data are collected over a long time and sources are
weak and/or overlapping. For transmission wavefields, the time axis
and the shot axis are naturally combined. If we assume that ns
individual sources, and the reflections that occur t seconds
afterward, are distributed at intervals within the total recording
time ![]() , field data can only be parameterized
, field data can only be parameterized ![]() . Both t and
. Both t and ![]() represent the real time axis, though I
will parameterize different wavefields with them with the understanding that
represent the real time axis, though I
will parameterize different wavefields with them with the understanding that
![]() is the two-way time to the deepest reflector of interest and
is the two-way time to the deepest reflector of interest and
![]() is the real time axis from the beginning to the end of the
total recording time such that
is the real time axis from the beginning to the end of the
total recording time such that
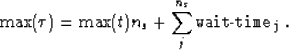 |
(2) |
Without knowing when sources happen, and acknowledging that the
wait-time between shots can also be negative, it is impossible to
separate field data into individual wavefields when attempting to
image with the ambient noisefield. In this case, equation 1
can only be implemented with a single time function of length ![]()
| |
(3) |
| (4) |
| |
(5) |
For passive field data, ![]() is
is ![]() , and the gn(t) are
, and the gn(t) are
![]() as well as background noise between
sources. Thus, correlating a single long recording from many sources
implicitly stacks the wavefields from individual sources at each
frequency. For passive data, the time axis and the shot axis are
combined in nature (by sources refusing to wait in turn) and in
processing (by seismologists incapable of or refusing to process
individual time windows). However, this transform only supports a
time signal of length t and is aliasing the long field record.
as well as background noise between
sources. Thus, correlating a single long recording from many sources
implicitly stacks the wavefields from individual sources at each
frequency. For passive data, the time axis and the shot axis are
combined in nature (by sources refusing to wait in turn) and in
processing (by seismologists incapable of or refusing to process
individual time windows). However, this transform only supports a
time signal of length t and is aliasing the long field record.
What of the intermediate frequencies ![]() that would be lost
by stacking the time windows? It is necessary to remove these. Fine
sampling in frequency carries information about the late time samples
of the signal's dual representation. After correlation, shot records
in the time domain must be windowed to remove late lag correlations
which are superpositions of correlations of the different sources
convolved with the earth model. These are completely uninterpretable
in terms of the desired product
that would be lost
by stacking the time windows? It is necessary to remove these. Fine
sampling in frequency carries information about the late time samples
of the signal's dual representation. After correlation, shot records
in the time domain must be windowed to remove late lag correlations
which are superpositions of correlations of the different sources
convolved with the earth model. These are completely uninterpretable
in terms of the desired product ![]() and will be
noise in further processing. If the result needs truncation after
inverse transform, it is more efficient to only transform the part of
the result desired.
and will be
noise in further processing. If the result needs truncation after
inverse transform, it is more efficient to only transform the part of
the result desired.
Time windowing has a Fourier dual operation. The Fourier sampling
theorem, solved for ![]() is
is
![]()
The left column of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a processing flow of a simple
time domain signal with a zoomed in view of each trace (the first
32nd of the axis) on the right. The top trace is the input
signal. The middle trace is its autocorrelation. The bottom trace
maintains a part of the autocorrelation result deemed important. To
compute the bottom trace, the input was subsampled by 8 in the
Fourier domain, multiplied by its conjugate, and inverse transformed.
To facilitate plotting, the trace was padded with zeros. Identical
results are obtained by time-domain stacking and Fourier domain
subsampling as long as the level of decimation does not alias the
acausal lags of the correlation into the positive lags.
shows a processing flow of a simple
time domain signal with a zoomed in view of each trace (the first
32nd of the axis) on the right. The top trace is the input
signal. The middle trace is its autocorrelation. The bottom trace
maintains a part of the autocorrelation result deemed important. To
compute the bottom trace, the input was subsampled by 8 in the
Fourier domain, multiplied by its conjugate, and inverse transformed.
To facilitate plotting, the trace was padded with zeros. Identical
results are obtained by time-domain stacking and Fourier domain
subsampling as long as the level of decimation does not alias the
acausal lags of the correlation into the positive lags.
|
freq
Figure 1 Right column is 32x zoom of left beginning at t=0. (top) Idealized signal of three identical subsurface sources. (middle) Autocorrelation. (bottom) Autocorrelation performed with every 8th frequency. Zero values are padded on the bottom trace to facilitate plotting. | 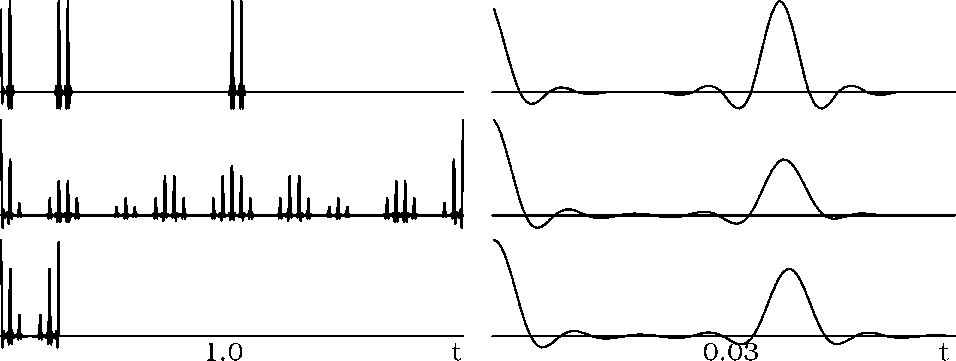 |
Subsampling in one domain is not an identical operation to windowing in
the dual domain. The periodicity of the Fourier transform dictates that
subsampling leads to aliasing rather than true truncation. Aliasing the
time domain is more efficiently performed by summing short time windows
before making the correlations and thereby greatly reducing the amount
of computation required. Knowing that the late time lags of
correlation are aphysical for passive imaging, the above analysis
shows that only the frequency samples at intervals ![]() ,
associated with records of length t, need to be inverse transformed
after correlation. Since correlation is linear, we only need to
calculate the frequency domain representation of the field data at
this reduced sampling interval. The definition of the DFT shows that
this is equivalent to first stacking the long time axis of the
data. The random background and instrument noise between sources is
diminished by the stacking of the time axis which also decimates a
potentially enormous data volume.
,
associated with records of length t, need to be inverse transformed
after correlation. Since correlation is linear, we only need to
calculate the frequency domain representation of the field data at
this reduced sampling interval. The definition of the DFT shows that
this is equivalent to first stacking the long time axis of the
data. The random background and instrument noise between sources is
diminished by the stacking of the time axis which also decimates a
potentially enormous data volume.
Under the assumption that all the source functions recorded in the
data are white and uncorrelated, the summation of the source
wavefields may not be to harmful and ![]() . Further,
if the sources are all continuously ringing, and thus zero-phase over
the recording, the correlations will not have residual phase. In my
previous reports, both of these assumptions were made (sometimes not
intentionally), which I now believe highly improbably for a real earth
experiment. To utilize bursts of local seismicity for imaging,
cross-correlating traces to make shot gathers makes
. Further,
if the sources are all continuously ringing, and thus zero-phase over
the recording, the correlations will not have residual phase. In my
previous reports, both of these assumptions were made (sometimes not
intentionally), which I now believe highly improbably for a real earth
experiment. To utilize bursts of local seismicity for imaging,
cross-correlating traces to make shot gathers makes ![]() . The situation is directly analogous to summing two or more
shot-records. While it may be useful for some applications, this sum
can not be treated as a single record with an impulsive source.
Cross-talk is introduced due to the inability to separate energy from
the distinct experiments.
. The situation is directly analogous to summing two or more
shot-records. While it may be useful for some applications, this sum
can not be treated as a single record with an impulsive source.
Cross-talk is introduced due to the inability to separate energy from
the distinct experiments.