Next: Subsurface-related domain: reflection angle
Up: Migration in complex areas
Previous: Migration in complex areas
Shot locations and offsets are parameterized according to their
location on the earth's surface where the seismic data is recorded.
Seismic processing using these surface-related coordinates
has been researched by geophysicists for decades. The kinematics of shot
domain common image gathers and offset domain image gathers are well understood
in constant velocity and v(z) media (, , ).
Difficulties arise when we begin considering complex subsurfaces with
rapid lateral velocity variations. Even in 2-D it is easy to construct
a model for which an individual common shot gather or common
offset gather can contain two events from two points in the subsurface
that arrive at the same time and are indistinguishable. In order to
examine such cases, let us first review basic survey geometry.
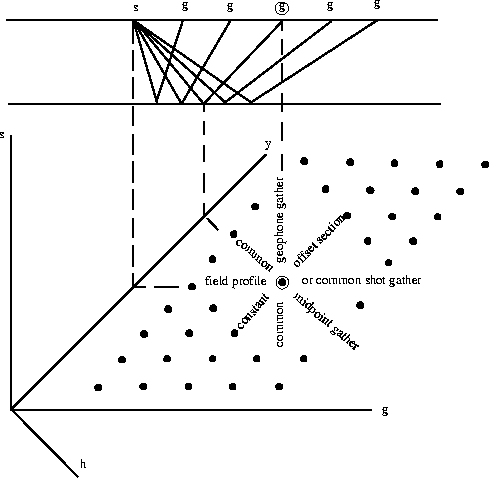
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , from (), shows the relationship between
the source, receiver, midpoint locations and offsets, as well as the
relationships between various common image gathers and common image
sections. The top part of Figure
, from (), shows the relationship between
the source, receiver, midpoint locations and offsets, as well as the
relationships between various common image gathers and common image
sections. The top part of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a simple survey
geometry over a single flat subsurface reflector: the single source (s)
is connected to each receiver (g) by rays that reflect at the flat
reflector. The lower part of Figure
shows a simple survey
geometry over a single flat subsurface reflector: the single source (s)
is connected to each receiver (g) by rays that reflect at the flat
reflector. The lower part of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows various ways we
can arrange the data based on the relation of the shot and receiver.
The axes are labeled to indicate the source location (s), receiver
location (g), offset (h) which is the difference between the receiver
and shot locations (1#1), and the midpoint location (y) which
is halfway between the source and receiver (2#2). Based on
this diagram, we can organize the raw data in many surface-related ways:
in common shot gathers, common receiver gathers, common midpoint gathers,
and constant offset sections.
shows various ways we
can arrange the data based on the relation of the shot and receiver.
The axes are labeled to indicate the source location (s), receiver
location (g), offset (h) which is the difference between the receiver
and shot locations (1#1), and the midpoint location (y) which
is halfway between the source and receiver (2#2). Based on
this diagram, we can organize the raw data in many surface-related ways:
in common shot gathers, common receiver gathers, common midpoint gathers,
and constant offset sections.
sg
Figure 1 The relationships of the surface-related parameters
source (s) and receiver (g) locations, and their sections and gathers.
The top part shows a simple survey
geometry over a single flat subsurface reflector: the single source (s)
is connected to each receiver (g) by rays that reflect at the flat reflector.
The lower part shows various ways we can arrange
the data based on the relation of the shot and receiver. The axes are
labeled to indicate the source location (s), receiver location (g),
offset (h) which is the difference between the receiver and shot locations
(1#1), and the midpoint location (y), which is halfway between the
source and receiver (2#2). (From ())

As seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
an individual common shot gather can be parameterized by the receiver location
r. If two raypaths between the same source and receiver exist such that
they have the same receiver ray parameter pr and the two-way
traveltime along each is the same, it is impossible to distinguish
between the two reflector locations ().
Figure
,
an individual common shot gather can be parameterized by the receiver location
r. If two raypaths between the same source and receiver exist such that
they have the same receiver ray parameter pr and the two-way
traveltime along each is the same, it is impossible to distinguish
between the two reflector locations ().
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a very simple case of this so-called multipathing.
shows a very simple case of this so-called multipathing.
shot1
Figure 2 Raypaths through a fairly simple velocity
model consisting of a weak vertical velocity gradient and a strong low
velocity lens. An individual shot gather will contain energy that travels
along both of these raypaths. The low velocity lens allows both traveltimes
and receiver ray parameters pr to be identical.
|
|  |

Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) also shows that an individual common offset gather
can be parameterized by midpoint m.
Suppose that the midpoint ray parameter pm = ps + pr is
the same for two raypaths with the same traveltimes. Once again,
the two raypaths represent the same data space event, and the location of the
reflector causing this event is ambiguous.
Figure
also shows that an individual common offset gather
can be parameterized by midpoint m.
Suppose that the midpoint ray parameter pm = ps + pr is
the same for two raypaths with the same traveltimes. Once again,
the two raypaths represent the same data space event, and the location of the
reflector causing this event is ambiguous.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a case of multipathing where ps1=-pr1
and ps2=-pr2 so that pm1=pm2=0.
shows a case of multipathing where ps1=-pr1
and ps2=-pr2 so that pm1=pm2=0.
offset1
Figure 3 Raypaths through a simple constant velocity
velocity model with a low velocity lens. An individual common offset
gather will contain energy that travels along both of these raypaths.
The arrivals will have identical traveltimes and midpoint ray parameters.
|
|  |

These simple cases clearly show that processing that uses these
surface-related domains can be easily tricked. If we limit ourselves
to the shot and offset domains, we may not be able to separate energy returning
to the surface from different points in the subsurface. Even worse,
we frequently want to try to extract additional information from the
model, such as rock properties from amplitude analysis. If our analyses
are carried out in surface-related coordinates such as offset, we will
be seeing not only effects of multipathing, but less severe effects
as the seismic energy passes through the subsurface between the surface and
the point we have defined in terms of common midpoint. Relying on
surface-related coordinates puts our analysis at the mercy of the
accuracy of our subsurface model, which was built based on imaging
methods using the surface-related coordinates itself. Fortunately,
we can turn to a subsurface-related domain: the reflection angle domain.





Next: Subsurface-related domain: reflection angle
Up: Migration in complex areas
Previous: Migration in complex areas
Stanford Exploration Project
10/31/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , from (), shows the relationship between
the source, receiver, midpoint locations and offsets, as well as the
relationships between various common image gathers and common image
sections. The top part of Figure
, from (), shows the relationship between
the source, receiver, midpoint locations and offsets, as well as the
relationships between various common image gathers and common image
sections. The top part of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a simple survey
geometry over a single flat subsurface reflector: the single source (s)
is connected to each receiver (g) by rays that reflect at the flat
reflector. The lower part of Figure
shows a simple survey
geometry over a single flat subsurface reflector: the single source (s)
is connected to each receiver (g) by rays that reflect at the flat
reflector. The lower part of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows various ways we
can arrange the data based on the relation of the shot and receiver.
The axes are labeled to indicate the source location (s), receiver
location (g), offset (h) which is the difference between the receiver
and shot locations (1#1), and the midpoint location (y) which
is halfway between the source and receiver (2#2). Based on
this diagram, we can organize the raw data in many surface-related ways:
in common shot gathers, common receiver gathers, common midpoint gathers,
and constant offset sections.
shows various ways we
can arrange the data based on the relation of the shot and receiver.
The axes are labeled to indicate the source location (s), receiver
location (g), offset (h) which is the difference between the receiver
and shot locations (1#1), and the midpoint location (y) which
is halfway between the source and receiver (2#2). Based on
this diagram, we can organize the raw data in many surface-related ways:
in common shot gathers, common receiver gathers, common midpoint gathers,
and constant offset sections.