| |
(114) |
| |
(115) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we have for the data vector d the following equalities:
), we have for the data vector d the following equalities:
| |
||
| (116) |
|
geom11
Figure 1 A geometric interpretation of the noise filter when n and s are not orthogonal. |  |
|
geom21
Figure 2 A geometric interpretation of the noise filter when n and s are orthogonal. |  |
| |
||
| (117) |
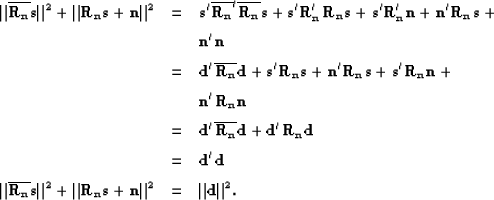 |
||
| (118) | ||
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
the last two equalities can be written as follows:
),
the last two equalities can be written as follows:
| |
||
| (119) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ;
similarly,
;
similarly, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Similarly, n is in the
null space of
). Similarly, n is in the
null space of