




Next: Adaptive subtraction
Up: Multiple subtraction
Previous: Multiple subtraction
The pattern-based approach separates noise and signal according to
their multivariate spectra. In this Chapter, the patterns are approximated with
3-D prediction-error filters (PEFs). Calling 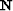 the PEFs for
the multiples estimated from the multiple model with SRMP,
the PEFs for
the multiples estimated from the multiple model with SRMP,  the PEFs for
the signal estimated from the Spitz approximation
Spitz (1999) and
the PEFs for
the signal estimated from the Spitz approximation
Spitz (1999) and  the primaries, the objective
function to minimize becomes
the primaries, the objective
function to minimize becomes
| 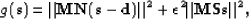 |
(70) |
where 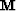 is a masking operator that preserves the signal where
no multiples are present. The signal is estimated iteratively with
a conjugate gradient method, and not with the Huber norm of Chapter
is a masking operator that preserves the signal where
no multiples are present. The signal is estimated iteratively with
a conjugate gradient method, and not with the Huber norm of Chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In few words, the Spitz approximation
consists in (1) convolving the noise PEFs N with the data
d, and (2) estimating the signal PEFs S from the convolution
result. As demonstrated by Abma (1995), the
least-squares inverse of
. In few words, the Spitz approximation
consists in (1) convolving the noise PEFs N with the data
d, and (2) estimating the signal PEFs S from the convolution
result. As demonstrated by Abma (1995), the
least-squares inverse of  in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
an optimal Wiener filter. Similar to Chapter
) is
an optimal Wiener filter. Similar to Chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the dataset is divided into macro-patches of 50
consecutive shots with an overlap of 5 shots before the
separation. Then the macro-patches are reassembled to form the final
result.
, the dataset is divided into macro-patches of 50
consecutive shots with an overlap of 5 shots before the
separation. Then the macro-patches are reassembled to form the final
result.





Next: Adaptive subtraction
Up: Multiple subtraction
Previous: Multiple subtraction
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In few words, the Spitz approximation
consists in (1) convolving the noise PEFs N with the data
d, and (2) estimating the signal PEFs S from the convolution
result. As demonstrated by Abma (1995), the
least-squares inverse of
. In few words, the Spitz approximation
consists in (1) convolving the noise PEFs N with the data
d, and (2) estimating the signal PEFs S from the convolution
result. As demonstrated by Abma (1995), the
least-squares inverse of ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
an optimal Wiener filter. Similar to Chapter
) is
an optimal Wiener filter. Similar to Chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the dataset is divided into macro-patches of 50
consecutive shots with an overlap of 5 shots before the
separation. Then the macro-patches are reassembled to form the final
result.
, the dataset is divided into macro-patches of 50
consecutive shots with an overlap of 5 shots before the
separation. Then the macro-patches are reassembled to form the final
result.