The Huber norm

Chapter introduces the Huber norm Huber (1973). The Huber norm is an hybrid 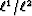$\ell^1/\ell^2$ error measure that is robust to outliers. Because it is differentiable everywhere, the Huber norm can be minimized with a gradient-based algorithm. In Chapter , I propose minimizing the Huber norm with a quasi-Newton method called L-BFGS. This technique can solve any non-linear problem where local-minima are sought. Its limited-memory requirements make it also very attractive for solving large-scale problems. On a velocity estimation problem, this Chapter illustrates that the Huber norm with the L-BFGS solver is robust to outliers, thus providing an alternative to the $\ell^1$ norm.