FEAVA removal

No approach attempted up to date has managed to successfully remove all FEAVA effects from ADCIGs. Hatchell (2000a) states that AVO stack (croscorrelate traces to get rid of the traveltime aspects of FEAVA, then stack) is effective in eliminating FEAVA from the stacked image. This, however, does not solve the problem of ``contaminated'' angle gather amplitudes which impedes AVA analysis.

Another avenue of approach consists of using the physics of FEAVO to generate a velocity/absorption anomaly section, and then to use it for imaging, which will eliminate FEAVO. Woodward (1987), Claerbout (1993), Bevc (1994), and Harlan (1994) follow the template laid out by Kjartansson (1979): (1) Generate a bidimensional midpoint-offset map of FEAVO effects as expressed in either the traveltime or the amplitude of unmigrated data. (2) Obtain the transmission anomaly section by inputting the map obtained at step 1 into an inverted operator. At first sight, the tomographic seismic amplitude correction in Harlan (1994) appears quite successful, managing to eliminate the FEAVO effects along particular well-defined reflectors one at a time by computing transmission anomaly sections used to correct the amplitudes. Nevertheless, he states that the transmission anomaly sections generated for different reflectors appear inconsistent, and that simultaneous inversion did not improve things. For ``cleaning'' the FEAVO effect the process must be repeated for each particular reflector, and it involves picking, a process prone to errors in the case of weaker reflectors. Most of these approaches suffered because of using ray theory, and all of them because they were working in the data domain, before migration eliminates other propagation effects. Also, none of them used all the FEAVO characteristics described in a previous section at the same time. Since this information is not redundant, all is necessary to properly characterize the FEAVO sources.

Vlad and Biondi (2002), Vlad (2002) and Vlad et al. (2003a) propose an approach that follows the strategy of finding a correct velocity model and imaging with it to get rid of FEAVO. Vlad (2004b) refine it further. This method proceeds as follows:

(1) Find the background velocity sufficiently well to flatten the ADCIGs, except for FEAVA effects.

(2) Perform prestack depth migration and transformation to ADCIGs.

(3) Process the ADCIGs so that in the end they contain only FEAVA effects, in the manner of Figure . Areas where no focusing effects are present are zeroed. In areas where FEAVA is overimposed with ``legitimate'', lithological AVA (everywhere else), the lithological AVA is found and subtracted, so that only FEAVA effects remain. The processed ADCIGs are called a ``image perturbation''.

(4) The image perturbation is transformed from ADCIGs to offset, fed into the adjoint of wavefield-extrapolation migration, then becomes input for inverse linearized downward continuation. The end product is a velocity update.

(5) The velocity field is updated and a new iteration proceeds.

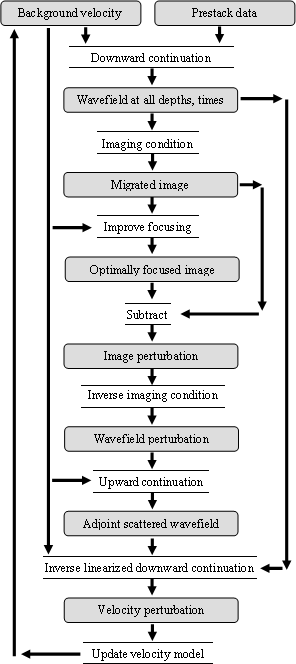
This is an adaptation of Wavefield-Extrapolation Migration Velocity Analysis (WEMVA), an iterative inversion method described by Sava (2004). Figure provides a flowchart. In essence, WEMVA linearizes and inverts the whole process of transforming a dataset and a velocity model into ADCIGs.

 

wemva Figure 15 WEMVA flowchart. From Vlad and Tisserant (2004).

This is a complex machinery which invites several questions. What can go wrong? How large are the errors introduced by the inverse linearized downward continuation? Vlad et al. (2003a) explore in detail the answers. Provided an optimal image perturbation (with the help of a synthetic dataset), WEMVA manages to produce velocity updates that eliminate FEAVO from the ADCIGs through migration. The only step left to accomplish is extracting the FEAVA-only image perturbation.

Vlad (2004b) deals specifically with this issue. The (revised since then) FEAVA extraction process from the ADCIGs consists of the following steps:

(1) Detect: Use the FEAVA detector to keep all that can possibly be FEAVA. Set a threshold and zero the rest of the values in the ADCIGs.

(2) Focus: Take the absolute value/envelope of the output of (1) and run a weighed summation operator along precomputed velocity-dependent FEAVA surfaces. Semblance will not work because it will be attracted by higher coherence along the reflectors. The summation weights will consider the finite spatial extent of the FEAVA effects and may be negative in the exterior according to the extent of the bright/dim zones predicted by theory.

(3) Filter the output of (2) in the manner of Harlan (1986) to keep only the high semblance values.

(4) Spread back along the FEAVA surfaces, with weights, to obtain a weighted mask that indicates the probability of FEAVA presence in any voxel in ADCIGs. Zero everything in ADCIGs outside the mask.

(5) Interpolate reflector-caused lithological AVO inside the mask from values outside the mask and geologic information.

(6) Subtract the output of (5) from the corresponding unaltered values in ADCIGs at the respective locations.

Needed: a working implementation of the image perturbation extraction process described above.

FEAVA effects are a suitable input for WEMVA because the small traveltime effects makes them satisfy easily the Born approximation required from WEMVA inputs. There are variations of WEMVA which are not subject to the Born constraints Sava and Symes (2002), but they incorporate the image perturbation extraction step inside the inversion process, making it difficult to isolate errors that may appear during the design and prototyping of the FEAVA extraction procedure described above.

WEMVA coupled with FEAVA extraction in the manner described above has many strengths that previous approaches did not have. It considers every aspect of FEAVO, it uses wavefield-extrapolation methods, and it takes the input of the inversion from the image domain. Potential weaknesses lay in the subjectivity associated with the image perturbation extraction, with the cost (each linear solver iteration contains a prestack downward continuation and a prestack upward continuation; several solver iterations are required for a single step of WEMVA.) and with the fact that it does not consider absorption, which is likely to exist in real data.