




Next: From ODCIGs to ADCIGs
Up: Shragge et al.: Forward-scattered
Previous: Shot-profile migration
In this section, we examine the ODCIG volumes generated by
forward-scattered wavefields. For simplicity, we illustrate these
concepts using plane-wave S and R wavefields. We
also assume that S and R propagate at constant, though not
necessarily equal, slownesses (i.e., reciprocal of velocity). These
idealizations allow us to generate an analytic surface in ODCIG space
for both P-P diffracted and P-S converted waves. We specify
planar S and R wavefields in constant velocity media using source
and receiver ray parameter vectors, 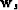 and
and 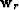 , defined by,
, defined by,
| ![\begin{displaymath}
\mathbf{w}_s=\left[p_s,q_s\right]= s_s \;\left[\;{\rm sin}\;...
...]= s_r \;\left[\;{\rm sin}\;\beta_r,{\rm cos}\;\beta_r\right],
\end{displaymath}](img17.gif) |
(3) |
where ps and pr are the source and receiver horizontal ray
parameters, qs and qr are the source and receiver vertical ray parameters, and
ss and sr are the source and receiver wavefield propagation
slownesses, respectively. Also, we use a convention where angles are
defined clockwise positive with respect to the vertical depth axis.
Forward-scattered S and R wavefields must satisfy the causality
arguments illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which requires
a negative sign in the source and receiver extrapolation operators.
Using the aforementioned assumptions, we generate the following
extrapolated S and R wavefield volumes,
, which requires
a negative sign in the source and receiver extrapolation operators.
Using the aforementioned assumptions, we generate the following
extrapolated S and R wavefield volumes,
| 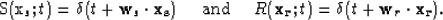 |
(4) |
Applying a Fourier transform over the t-axis of both S and R yields,
| 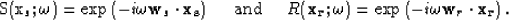 |
(5) |
Evaluating the imaging condition in Equation (2)
with the wavefields in Equation (5) generates the
following image-space volume,
| ![\begin{eqnarray}
I(\mathbf{x},\mathbf{h}) = & \sum_{\omega} \delta(\mathbf{x_s...
...) + \mathbf{h}\cdot(\mathbf{w}_s+\mathbf{w}_r) \right]. \nonumber
\end{eqnarray}](img20.gif) |
|
| (6) |
| |
The non-zero 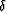 -function argument,
-function argument,
| 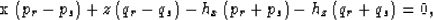 |
(7) |
represents an analytic forward-scattered ODCIG hyper-plane surface.
Importantly, this surface interrelates source and receiver
plane-wave angles, propagation slownesses and image-space variables,
 and
and 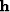 . In the next section, we manipulate this formula
to generate constraint equations that help isolate the receiver-side
contribution to the total reflection angle.
. In the next section, we manipulate this formula
to generate constraint equations that help isolate the receiver-side
contribution to the total reflection angle.





Next: From ODCIGs to ADCIGs
Up: Shragge et al.: Forward-scattered
Previous: Shot-profile migration
Stanford Exploration Project
5/3/2005
![]() and
and ![]() , defined by,
, defined by,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which requires
a negative sign in the source and receiver extrapolation operators.
Using the aforementioned assumptions, we generate the following
extrapolated S and R wavefield volumes,
, which requires
a negative sign in the source and receiver extrapolation operators.
Using the aforementioned assumptions, we generate the following
extrapolated S and R wavefield volumes,
![\begin{eqnarray}
I(\mathbf{x},\mathbf{h}) = & \sum_{\omega} \delta(\mathbf{x_s...
...) + \mathbf{h}\cdot(\mathbf{w}_s+\mathbf{w}_r) \right]. \nonumber
\end{eqnarray}](img20.gif)