Next: Discussion and Future Work
Up: Numerical Examples
Previous: 2D Example - Canadian
Using the elevation map of the San Francisco Bay area illustrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a second test was conducted to assess the
applicability of the method in 3D. The maximum surface topographic
relief is approximately 800 m; however, the elevation gradients and
topographic wavelengths are significantly smaller and longer than the 2D
test illustrated in Figure
, a second test was conducted to assess the
applicability of the method in 3D. The maximum surface topographic
relief is approximately 800 m; however, the elevation gradients and
topographic wavelengths are significantly smaller and longer than the 2D
test illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The flat
subsurface datum is set a depth of 8000 m.
. The flat
subsurface datum is set a depth of 8000 m.
Bay.2D
Figure 4 Elevation map of the San Francisco Bay
area used in 3D testing.
|
|  |





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the slices through the 3D potential
function results. The top panel shows a depth slice at approximately
zero elevation, whereas the lower two panels show slices along Easting
(bottom left) and Southing (bottom right) directions.
presents the slices through the 3D potential
function results. The top panel shows a depth slice at approximately
zero elevation, whereas the lower two panels show slices along Easting
(bottom left) and Southing (bottom right) directions.
Pot3D
Figure 5 3D potential function for San Francisco Bay
area topography. a) depth slice of the potential function
at approximately zero elevation; b) vertical slice along
Southing 20 km; and c) vertical slice along Easting 20 km.
Note that the potential function is smoother than the
previous example indicating less coordinate system focusing.





These profiles illustrate a PF that is smoother than the previous
example.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the coordinate system generated along
the same two slices shown in the panels b) and c) of
shows the coordinate system generated along
the same two slices shown in the panels b) and c) of
Ray.slice
Figure 6 Cross-section of the 3-D coordinate system
developed for the San Francisco Bay area topography. Left-hand
panel: vertical slice along along Southing 20 km; and right-hand
panel: vertical slice along Easting 20 km.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The generated coordinate system much smoother
than in the previous example, as expected from the smoothness of the
PF. Figure
. The generated coordinate system much smoother
than in the previous example, as expected from the smoothness of the
PF. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a perspective view of the ray-traced
coordinate system results.
presents a perspective view of the ray-traced
coordinate system results.
Rays3D
Figure 7 Perspective view of the ray-traced coordinate
system developed from potential function in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





The coordinate system rays are fairly straight, except in the region
beneath topographic highs. Another way to visualize the ray
coordinate system is to examine how the topography 'heals itself' at
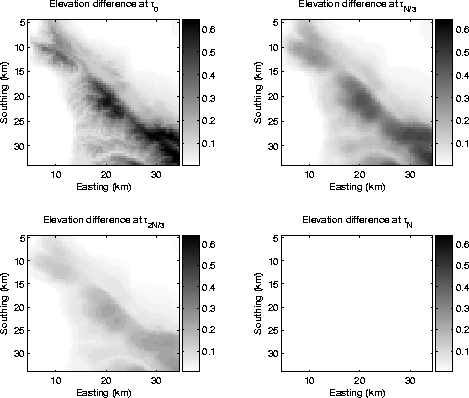
various  steps. Figure
steps. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this for
the
illustrates this for
the 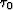 (top left),
(top left), 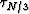 (top right),
(top right), 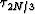 (bottom left) and
(bottom left) and 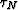 (bottom right) surfaces, where N is the
total number of extrapolation steps.
(bottom right) surfaces, where N is the
total number of extrapolation steps.
Rays3D2
Figure 8 Illustration of topographic coordinate
system healing through examination of single-extrapolation step elevation
differences (in km). Top left: step 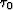 ; top right: step
; top right: step
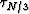 ; bottom left: step
; bottom left: step 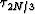 ; and bottom right:
step
; and bottom right:
step 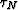 . Sidebar shows the elevation differences (in km), where the
greyscale has clipped according to the peak elevation difference at
. Sidebar shows the elevation differences (in km), where the
greyscale has clipped according to the peak elevation difference at
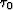 .
.





The sidebars show the elevation difference between the
lowest and highest points of each equipotential surface. The
greyscale intensity has been clipped according to the maximum
elevation difference at 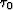 .
.





Next: Discussion and Future Work
Up: Numerical Examples
Previous: 2D Example - Canadian
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a second test was conducted to assess the
applicability of the method in 3D. The maximum surface topographic
relief is approximately 800 m; however, the elevation gradients and
topographic wavelengths are significantly smaller and longer than the 2D
test illustrated in Figure
, a second test was conducted to assess the
applicability of the method in 3D. The maximum surface topographic
relief is approximately 800 m; however, the elevation gradients and
topographic wavelengths are significantly smaller and longer than the 2D
test illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The flat
subsurface datum is set a depth of 8000 m.
. The flat
subsurface datum is set a depth of 8000 m.