




Next: discussion and conclusion
Up: Wang and Shan: Imaging
Previous: Wavefield propagator
The macro-velocity field has a decisive influence on seismic-wave imaging. Unfortunately, it is not easy to accurately estimate the velocity field from the seismic data. Up to now, the residual depth/time difference in the common-image gathers has been used for migration-velocity analysis (MVA) or inverting the macro-velocity distribution. However, in the case of complex topography and gelogical structures, MVA is not a successful approach. Therefore, seismic-wave imaging in complex survey areas has a long way to go.
We propose the following approach to inverting the macro-velocity field. The norm is defined as
| 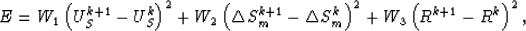 |
(48) |
where k stands for the iterative number; US is the calculated scattering wavefield. R is the position of the main reflectors, which can be identified from the migrated profile. 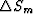 is the slowness disturbance field. W1,W2 and W3 are the different weights.
According to Bleistein (2000,p.39), the calculated scattering wavefield can be given by
is the slowness disturbance field. W1,W2 and W3 are the different weights.
According to Bleistein (2000,p.39), the calculated scattering wavefield can be given by
| 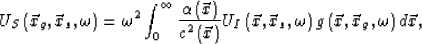 |
(49) |
where 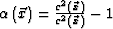 .Alternatively, the calculated scattering wavefield () also can be given by
.Alternatively, the calculated scattering wavefield () also can be given by
| ![\begin{displaymath}
\frac{\partial U_{S}\left(\omega, k_{x}, k_{y}, z \right) }{...
...left(x,y,z \right) U_{I}\left( \omega, x, y, z\right) \right] ,\end{displaymath}](img109.gif) |
(50) |
where 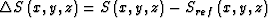 is the slowness disturbance, UI is the incident wave field, and kz is the vertical wavenumber. The incident wave field UI can be calculated with the following equation:
is the slowness disturbance, UI is the incident wave field, and kz is the vertical wavenumber. The incident wave field UI can be calculated with the following equation:
| 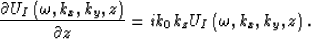 |
(51) |
where 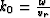 ,
, 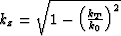 and
and 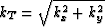 .
.





Next: discussion and conclusion
Up: Wang and Shan: Imaging
Previous: Wavefield propagator
Stanford Exploration Project
5/3/2005