




Next: Self-adaptive Reference velocity choice
Up: Wang and Shan: Choosing
Previous: Introduction
The Single-Square-Root (SSR) wavefield-extrapolation equation in the case of lateral velocity variation is of the following form Claerbout (1985):
| 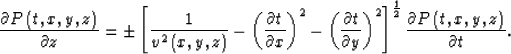 |
(1) |
The sign convention for the square root is negative for upcoming wavefield and positive for downgoing wavefield. We decompose the velocity field into two parts: the background velocity field and the velocity perturbation. In fact, we process the slowness field because the decomposition of the slowness is linear. The slowness field decomposition is defined as follows:
| 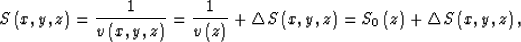 |
(2) |
where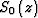 is the background slowness,
is the background slowness, 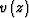 the background velocity and
the background velocity and 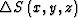 is the slowness perturbation. We hope that the velocity perturbation
is the slowness perturbation. We hope that the velocity perturbation 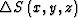 is as small as possible. Substituting the slowness-field-decomposition equation (2) into the wavefield-depth-extrapolation equation (1) and discarding the second-order terms of the slowness perturbation yields the following formula:
is as small as possible. Substituting the slowness-field-decomposition equation (2) into the wavefield-depth-extrapolation equation (1) and discarding the second-order terms of the slowness perturbation yields the following formula:
| 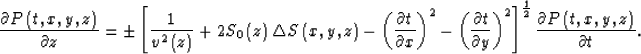 |
(3) |
Equation (3) can be rewritten as follows:
| 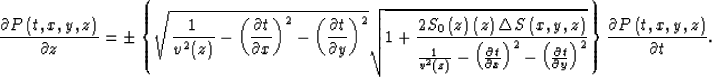 |
(4) |
In simplicity, we define 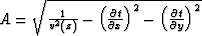 .
Taylor-series expansion of the second square-root term in equation (4), neglecting second- and higher-order terms, yields
.
Taylor-series expansion of the second square-root term in equation (4), neglecting second- and higher-order terms, yields
| 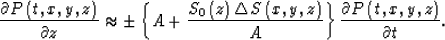 |
(5) |
Meanwhile, equation (5) can be rearranged as follows:
| ![\begin{eqnarray}
\frac{\partial P\left( t,x,y,z\right) }{\partial z}=
&\pm &\le...
... S\left( x,y,z\right)P\left( t,x,y,z\right) \right] }{\partial t}.\end{eqnarray}](img10.gif) |
|
| (6) |
Transforming equation (6) into frequency-wavenumber domain gives
| ![\begin{displaymath}
\frac{\partial P\left( \omega,k_{x},k_{y};z\right) }
{\part...
...gle S\left( x,y,z\right) P\left(\omega,x,y;z \right)
\right],\end{displaymath}](img11.gif) |
(7) |
where 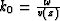 ,
, 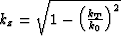 ,
, 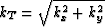 .
.
Equation (7) can be split into two equations:
| 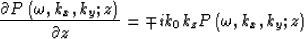 |
(8) |
and
| ![\begin{displaymath}
\frac{
\partial P\left( \omega,k_{x},k_{y};z\right)
}{\pa...
...ngle S\left( x,y,z\right) P\left(\omega,x,y;z \right)
\right].\end{displaymath}](img16.gif) |
(9) |
Equation (8) downward extrapolates the wave field in the background velocity. Equation (9) describes the scattering wave propagation, which is caused by the slowness perturbation. The total wavefield is the summation of the background and scattering wavefields.
When the vertical wavenumber kz approaches zero, equation (9) has a singular point. To circumvent the problem, 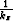 is expanded into a Taylor series:
is expanded into a Taylor series:
| 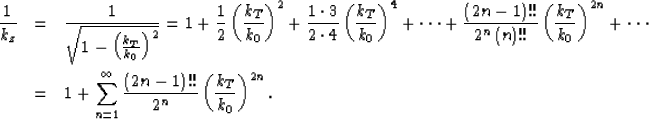 |
|
| (10) |
Substituting formula (10) into equation (9) gives,
| ![\begin{eqnarray}
\frac{\partial P\left( \omega,k_{x},k_{y},z\right) }{\partial z...
...iangle S\left( x,y,z\right) P\left(\omega,x,y;z \right)
\right].\end{eqnarray}](img19.gif) |
|
| |
| (11) |
Equation (11) is also split into two equations:
| 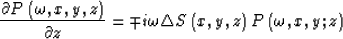 |
(12) |
and
| ![\begin{displaymath}
\frac{\partial P\left( \omega,k_{x},k_{y},z\right) }{\partia...
...gle S\left( x,y,z\right) P\left(\omega,x,y;z \right)
\right].\end{displaymath}](img21.gif) |
(13) |
In the case of narrow propagation angles (near zero degree), 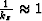 is satisfied, and equations (8) and (9) degrade to the split-step Fourier propagator (Stoffa, 1990):
is satisfied, and equations (8) and (9) degrade to the split-step Fourier propagator (Stoffa, 1990):
| 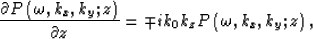 |
(14) |
| 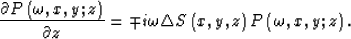 |
(15) |
Equations (8), (12) and (13) are combined to form the GSP (Huang et al, 1999).
We can see that equation (13) deals with the wave propagation at high angles, which can be processed in either the frequency wavenumber domain (with the GSP operator) or frequency space domain (with the FFD operator).
From the above derivation, we can see that the high-order terms of the slowness perturbation have been discarded twice, which works only under the condition of small slowness perturbation. Therefore, the slowness perturbation 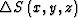 should be as small as possible. However, using the velocity value at each spatial point as a reference velocity is impractical in calculation. Generally, the slowness perturbation is defined as
should be as small as possible. However, using the velocity value at each spatial point as a reference velocity is impractical in calculation. Generally, the slowness perturbation is defined as
| 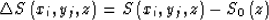 |
(16) |
We need to choose a set of reference velocities in an extrapolation step to maximize the accuracy of wave propagation.





Next: Self-adaptive Reference velocity choice
Up: Wang and Shan: Choosing
Previous: Introduction
Stanford Exploration Project
5/3/2005
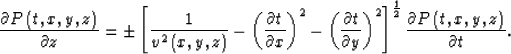
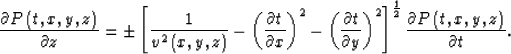
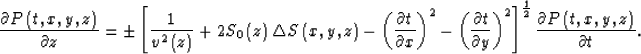
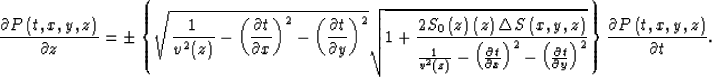
![\begin{eqnarray}
\frac{\partial P\left( t,x,y,z\right) }{\partial z}=
&\pm &\le...
... S\left( x,y,z\right)P\left( t,x,y,z\right) \right] }{\partial t}.\end{eqnarray}](img10.gif)
![]() is expanded into a Taylor series:
is expanded into a Taylor series:
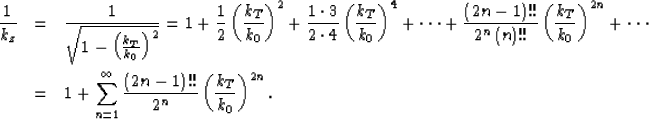
![\begin{eqnarray}
\frac{\partial P\left( \omega,k_{x},k_{y},z\right) }{\partial z...
...iangle S\left( x,y,z\right) P\left(\omega,x,y;z \right)
\right].\end{eqnarray}](img19.gif)
![]() is satisfied, and equations (8) and (9) degrade to the split-step Fourier propagator (Stoffa, 1990):
is satisfied, and equations (8) and (9) degrade to the split-step Fourier propagator (Stoffa, 1990):
![]() should be as small as possible. However, using the velocity value at each spatial point as a reference velocity is impractical in calculation. Generally, the slowness perturbation is defined as
should be as small as possible. However, using the velocity value at each spatial point as a reference velocity is impractical in calculation. Generally, the slowness perturbation is defined as