




Next: Anisotropic plane-wave migration in
Up: Shan and Biondi: Steeply
Previous: Introduction
A VTI medium is a medium that is transversely isotropic and has a vertical
axis of symmetry. The phase-velocity 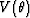 of P-waves in VTI media can be expressed
in Thomsen notation as follows Tsvankin (1996):
of P-waves in VTI media can be expressed
in Thomsen notation as follows Tsvankin (1996):
| 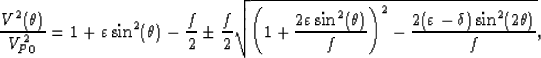 |
(1) |
where 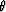 is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0
are the P- and SV-wave velocities in the vertical direction, respectively, and
is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0
are the P- and SV-wave velocities in the vertical direction, respectively, and  and
and 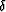 are anisotropy parameters defined by Thomsen (1986):
are anisotropy parameters defined by Thomsen (1986):
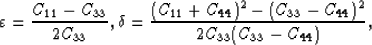
where Cij are elastic moduli. In equation (1), 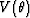 is the P-wave phase-velocity when the sign in front of the square root is positive,
and the SV-wave phase velocity for a negative sign.
is the P-wave phase-velocity when the sign in front of the square root is positive,
and the SV-wave phase velocity for a negative sign.
For plane-wave propagation, the phase angle 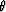 is related to the wavenumbers kx and kz by the following
relations:
is related to the wavenumbers kx and kz by the following
relations:
|  |
(2) |
where 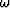 is the temporal frequency. From Cartesian coordinates to tilted
coordinates, we do a transformation as follows:
is the temporal frequency. From Cartesian coordinates to tilted
coordinates, we do a transformation as follows:
| 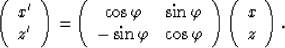 |
(3) |
where 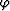 is the rotation angle.
is the rotation angle.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this change of symmetry axis during the coordinate transformation. The layered structure has a symmetry
axis in the vertical direction in Cartesian coordinates (x,z) in the left panel. When we rotate the coordinates from
(x,z) to
illustrates this change of symmetry axis during the coordinate transformation. The layered structure has a symmetry
axis in the vertical direction in Cartesian coordinates (x,z) in the left panel. When we rotate the coordinates from
(x,z) to 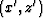 , the symmetry axis in the new coordinates
, the symmetry axis in the new coordinates 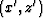 deviates from
the
deviates from
the 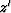 direction.
direction.
In tilted coordinates 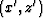 , we have the following relation between wavenumber
, we have the following relation between wavenumber 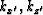 and phase angle
and phase angle 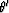 :
:
|  |
(4) |
The symmetry axis is not vertical in tilted coordinates, so the angle between the direction of wave propagation and the symmetry axis
is not the phase angle 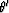 , but
, but 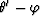 , where
, where
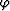 is the tilting angle of the tilted coordinates..
Therefore, VTI media in Cartesian coordinates become tilted TI media. The P-wave phase velocity in tilted coordinates can be expressed
as
is the tilting angle of the tilted coordinates..
Therefore, VTI media in Cartesian coordinates become tilted TI media. The P-wave phase velocity in tilted coordinates can be expressed
as
| 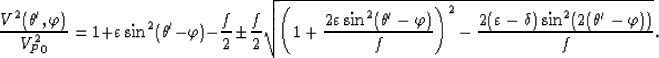 |
(5) |
vtitilt
Figure 1 VTI media in tilted coordinates. Left panel is a layer structure in Cartesian coordinates.
Right panel is the layer structure in tilted coordinates.

Thus for a VTI medium in tilted coordinates we need a wave-extrapolation operator that can downward extrapolate the
wavefield in tilted TI media. From equations (4) and (5), we can solve 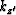 as
a function of
as
a function of 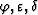 , and
, and 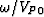 . The wavefield can be extrapolated in two steps.
First,
the wavefield is extrapolated by an isotropic operator as follows:
. The wavefield can be extrapolated in two steps.
First,
the wavefield is extrapolated by an isotropic operator as follows:
| 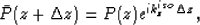 |
(6) |
where 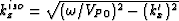 is the isotropic vertical spatial wavenumber. This isotropic operator can be implemented
by the split-step method Stoffa et al. (1990),
the general screen propagator Huang and Wu (1996),
or Fourier finite difference (FFD) Ristow and Ruhl (1994).
Next, the wavefield is corrected by an explicit correction operator.
This correction operator is designed in the Fourier domain, and is
implemented in the space domain.
The correction
operator in the Fourier domain is a phase-shift operator:
is the isotropic vertical spatial wavenumber. This isotropic operator can be implemented
by the split-step method Stoffa et al. (1990),
the general screen propagator Huang and Wu (1996),
or Fourier finite difference (FFD) Ristow and Ruhl (1994).
Next, the wavefield is corrected by an explicit correction operator.
This correction operator is designed in the Fourier domain, and is
implemented in the space domain.
The correction
operator in the Fourier domain is a phase-shift operator:
| 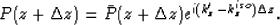 |
(7) |
In the space domain, this correction operator is a convolution filter. The coefficients of the convolution filter depend on
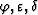 , and
, and 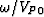 , and they can be estimated
by the weighted least-squares method Shan and Biondi (2004b).
, and they can be estimated
by the weighted least-squares method Shan and Biondi (2004b).





Next: Anisotropic plane-wave migration in
Up: Shan and Biondi: Steeply
Previous: Introduction
Stanford Exploration Project
5/3/2005
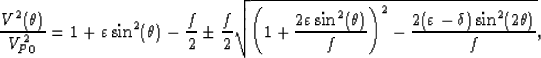
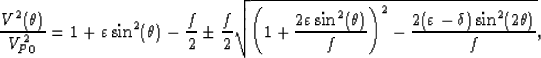
![]()
![]() is related to the wavenumbers kx and kz by the following
relations:
is related to the wavenumbers kx and kz by the following
relations:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this change of symmetry axis during the coordinate transformation. The layered structure has a symmetry
axis in the vertical direction in Cartesian coordinates (x,z) in the left panel. When we rotate the coordinates from
(x,z) to
illustrates this change of symmetry axis during the coordinate transformation. The layered structure has a symmetry
axis in the vertical direction in Cartesian coordinates (x,z) in the left panel. When we rotate the coordinates from
(x,z) to ![]() , the symmetry axis in the new coordinates
, the symmetry axis in the new coordinates ![]() deviates from
the
deviates from
the ![]() direction.
direction.
![]() , we have the following relation between wavenumber
, we have the following relation between wavenumber ![]() and phase angle
and phase angle ![]() :
:
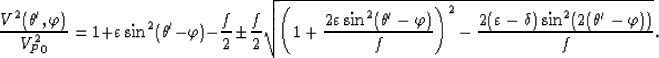

![]() as
a function of
as
a function of ![]() , and
, and ![]() . The wavefield can be extrapolated in two steps.
First,
the wavefield is extrapolated by an isotropic operator as follows:
. The wavefield can be extrapolated in two steps.
First,
the wavefield is extrapolated by an isotropic operator as follows: