




Next: Water-bottom multiple in Image
Up: Kinematics of Multiples in
Previous: Water-bottom multiples
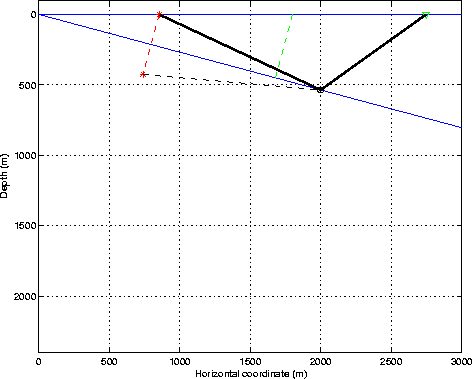
Consider now a diffractor sitting on top of the water-bottom reflector at the lateral
position xd and depth zd (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The moveout of the
primary diffraction is given by
). The moveout of the
primary diffraction is given by
| ![\begin{displaymath}
t_d=t_s+t_g=\frac{1}{V}\left[\sqrt{(x_d-m_D+h_D)^2+z_d^2}+\sqrt{(m_D+h_D-x_d)^2+x_d^2}\right]\end{displaymath}](img8.gif) |
(3) |
where ts and tg are traveltimes from the source and receiver to the
diffractor, respectively, mD is the horizontal position of the CMP gather and
hD is the half-offset between the source and the receiver.
This is the equation of a hyperbola with apex at the horizontal position directly
above the diffractor.
rayprimdiff
Figure 5 Image source construction for the
primary diffraction.
|
|  |





Consider now the multiple that hits the diffractor on its second bounce on the
dipping reflector (source-side multiple), as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This multiple is no longer the equivalent of any primary, but we can compute its
traveltime in the following way:
.
This multiple is no longer the equivalent of any primary, but we can compute its
traveltime in the following way:
- 1.
- Form the image source.
- 2.
- Find the point at the surface such that the lines joining that point
with both the image source and the diffractor intercept with the same
angle with respect to the vertical (Snell's law).
- 3.
- Compute the raypath using the law of cosines and divide by the velocity to
get the traveltime.
The coordinates of the image source (Xis,Zis) are given by
| 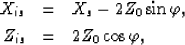 |
(4) |
| (5) |
where
| 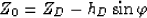 |
(6) |
is the perpendicular distance between the shot and the reflector.
raymuldiff
Figure 6 Diffracted multiple. Notice that
the last leg of the multiple does not satisfy Snell's law.
|
| 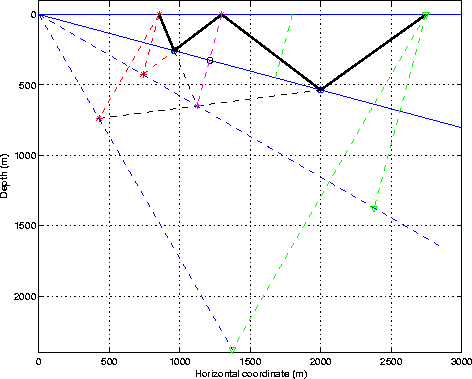 |





From the description of numeral 3. above, the surface coordinate of the multiple
bounce at the surface is:
| 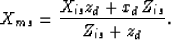 |
(7) |
The aperture angle of the first bounce of the multiple is 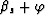 where
where 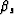 is the takeoff angle of the multiple with respect to the vertical.
The aperture angle at the surface bounce is
is the takeoff angle of the multiple with respect to the vertical.
The aperture angle at the surface bounce is 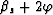 and can be easily
computed as
and can be easily
computed as
| 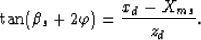 |
(8) |
The traveltime of the first leg of the multiple, in terms of 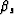 and the
vertical distance between the source and the reflector,
and the
vertical distance between the source and the reflector,
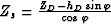 , is:
, is:
| 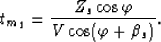 |
(9) |
Similarly, repeated application of the law of sines gives the traveltime of
the other three legs of the multiple
| 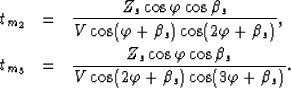 |
(10) |
| (11) |
The total arrival time of the diffracted multiple is therefore:
| 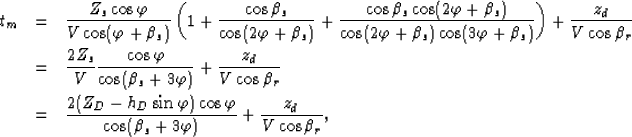 |
|
| |
| (12) |
where 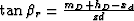 and
and 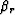 is the emergence angle of
the diffracted multiple with respect to the vertical. Figure
is the emergence angle of
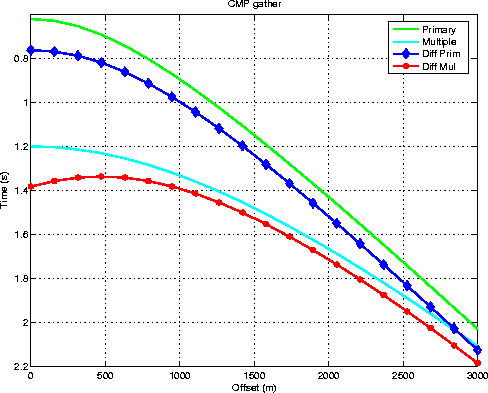
the diffracted multiple with respect to the vertical. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the moveout of the diffracted multiple with that of the water-bottom
multiple. Obviously, the apex of the diffracted multiple is not at zero offset.
compares the moveout of the diffracted multiple with that of the water-bottom
multiple. Obviously, the apex of the diffracted multiple is not at zero offset.
moveouts3
Figure 7 Moveout curves of primary,
water-bottom multiple, diffraction and diffracted multiple from a dipping
interface on a CMP gather.
|
|  |










Next: Water-bottom multiple in Image
Up: Kinematics of Multiples in
Previous: Water-bottom multiples
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The moveout of the
primary diffraction is given by
). The moveout of the
primary diffraction is given by

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This multiple is no longer the equivalent of any primary, but we can compute its
traveltime in the following way:
.
This multiple is no longer the equivalent of any primary, but we can compute its
traveltime in the following way:

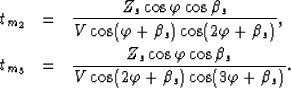
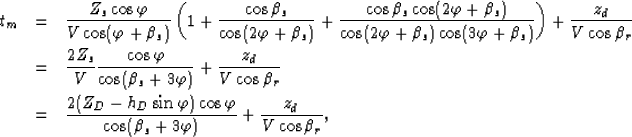
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the moveout of the diffracted multiple with that of the water-bottom
multiple. Obviously, the apex of the diffracted multiple is not at zero offset.
compares the moveout of the diffracted multiple with that of the water-bottom
multiple. Obviously, the apex of the diffracted multiple is not at zero offset.
