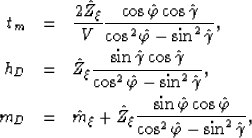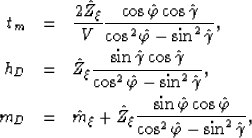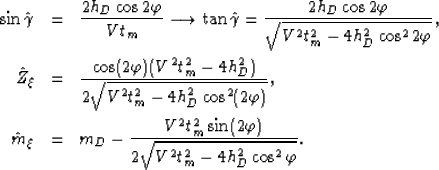Next: 2D Synthetic data example
Up: Alvarez: Kinematics of multiples
Previous: Diffracted multiples
Given the kinematic equivalence between the water-bottom multiple and a primary
from a reflector dipping at twice the dip angle, we can express the image space
coordinates of the water-bottom multiple in terms of the data space coordinates
by solving the system of equations presented by Fomel and Prucha
1999:
| 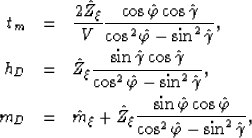 |
(13) |
| (14) |
| (15) |
where 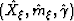 are the image space coordinates of the
primary that is kinematically equivalent to the first order water-bottom multiple as
mentioned n the previous section and
are the image space coordinates of the
primary that is kinematically equivalent to the first order water-bottom multiple as
mentioned n the previous section and 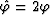 . The formal solution of
these equations, for the image space coordinates is:
. The formal solution of
these equations, for the image space coordinates is:
| 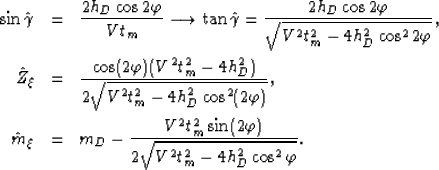 |
(16) |
| (17) |
| (18) |
These equations allow the computation of the impulse response of the
water-bottom multiples in image space as a function of the aperture angle. More
importantly, they are the starting
point for understanding the kinematics of the data in 3D ADCIGs Tisserant and Biondi (2004),
still a subject of research.





Next: 2D Synthetic data example
Up: Alvarez: Kinematics of multiples
Previous: Diffracted multiples
Stanford Exploration Project
5/3/2005