| (107) |
Using the chain rule of differentiation, we can write
| |
(108) |
dR offers the possibility to build the image
perturbation directly, by computing three elements:
the derivative of the image with respect to the depth wavenumber,
and two weighting functions, one for the derivative
of the depth wavenumber with respect to the velocity ratio parameter (![]() ),
and the other one for the magnitude of the
),
and the other one for the magnitude of the ![]() perturbation from the
reference to the improved image.
perturbation from the
reference to the improved image.
Firstly, the image derivative in the Fourier domain,
![]() ,
is straightforward to compute in the space domain as
,
is straightforward to compute in the space domain as
| (109) |
Secondly, we can obtain the weighting representing the derivative of
the depth wavenumber with respect to the velocity ratio parameter,
![]() , starting from
the double square root (DSR)
equation written for prestack Stolt residual migration
(87):
, starting from
the double square root (DSR)
equation written for prestack Stolt residual migration
(87):
&=& _s+ _r
&=& 12 ^2 ^2 - |k_s|^2
+ 12 ^2 ^2 - |k_r|^2 ,
where ![]() is given by the expression:
is given by the expression:
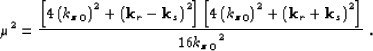 |
(110) |
The derivative of ![]() with respect to
with respect to ![]() is
is
| (111) |
| (112) |
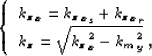 |
(113) |
_x_s &=& 12 ^2 _c^2 - k_m_x-k_h_x^2
_x_r &=& 12 ^2 _c^2 - k_m_x+k_h_x^2 ,
and ![]() is given by the expression:
is given by the expression:
| (114) |
d d
&=&
d d _x
d _xd
&=&
_x
_c^24_x_s + _c^24_x_r .
| (115) |