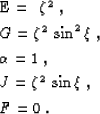Next: One-way wave-equation
Up: Riemannian wavefield extrapolation
Previous: Introduction
The acoustic propagation of a monochromatic wave is
governed by the Helmholtz equation:
| 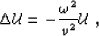 |
(1) |
where  is temporal frequency,
v is the spatially variable wave propagation velocity, and
is temporal frequency,
v is the spatially variable wave propagation velocity, and
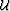 represents a wavefield.
represents a wavefield.
The Laplacian operator acting on a scalar function
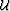 in an arbitrary Riemannian space with coordinates
in an arbitrary Riemannian space with coordinates
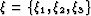 takes the form
takes the form
| 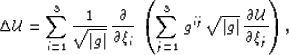 |
(2) |
where gij is a component of the associated metric tensor,
and 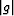 is its determinant (106).
The differential geometry of any coordinate system is
fully represented by the metric tensor gij.
is its determinant (106).
The differential geometry of any coordinate system is
fully represented by the metric tensor gij.
The expression simplifies if one of the coordinates,
e.g. the coordinate of one-way wave extrapolation 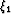 ,is orthogonal to the other coordinates
,is orthogonal to the other coordinates 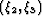 .
The metric tensor reduces to
.
The metric tensor reduces to
| ![\begin{displaymath}
\left[g_{ij}\right] = \lb\bea{ccc}
E& F& 0 \\ F& G& 0 \\ 0 & 0 & \AA^2
\eea\rb\;,\end{displaymath}](img10.gif) |
(3) |
where E, F, G, and  are differential forms that can be found
from mapping Cartesian coordinates
are differential forms that can be found
from mapping Cartesian coordinates 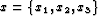 to general Riemannian coordinates
to general Riemannian coordinates 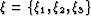 ,
as follows:
,
as follows:
E& = & _k _k _k ,
F& = & _k _k _k ,
G& = & _k _k _k ,
Å^2 & = & _k _k _k .
The associated metric tensor
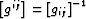 has the matrix
has the matrix
| 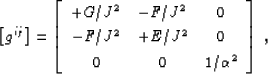 |
(4) |
where 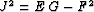 .
The metric determinant takes the form
.
The metric determinant takes the form
| 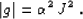 |
(5) |
Substituting ametric and det into laplac,
and making the notations
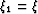 ,
, 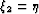 , and
, and 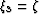 ,
with
,
with 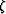 orthogonal to both
orthogonal to both 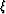 and
and 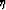 ,we obtain the Helmholtz wave helm
for propagating waves in a 3D semi-orthogonal Riemannian space:
1ÅJ
,we obtain the Helmholtz wave helm
for propagating waves in a 3D semi-orthogonal Riemannian space:
1ÅJ
JÅ
+
GÅJ -
FÅJ
+
EÅJ -
FÅJ
= - ^2v^2 .
In weqrc.3d, 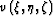 is the wave propagation velocity mapped to Riemannian coordinates.
is the wave propagation velocity mapped to Riemannian coordinates.
For the special case of two dimensional spaces
(F=0 and G=1),
the Helmholtz wave equation reduces to the simpler form:
| 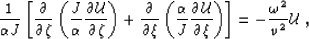 |
(6) |
which corresponds to a curvilinear orthogonal coordinate system.
Particular examples of coordinate systems for one-way wave propagation are:
- Cartesian (propagation in depth):
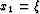 ,
, 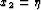 ,
, 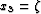 ,
,
- Cylindrical (propagation in radius):
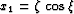 ,
, 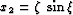 ,
, 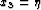 ,
,
- Spherical (propagation in radius):
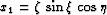 ,
, 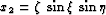 ,
, 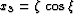 ,
,
- Ray family (propagation along rays):
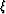 and
and 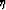 represent
parameters defining a particular ray in the family (i.e. the ray take-off
angles), J is the geometrical spreading factor, related to the
cross-sectional area of the ray tube (19). The coefficients
E, F, G, and J are easily computed by
finite-difference approximations
with the Huygens wavefront tracing technique (92). If
the propagation parameter
represent
parameters defining a particular ray in the family (i.e. the ray take-off
angles), J is the geometrical spreading factor, related to the
cross-sectional area of the ray tube (19). The coefficients
E, F, G, and J are easily computed by
finite-difference approximations
with the Huygens wavefront tracing technique (92). If
the propagation parameter 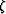 is taken to be time along the ray, then
is taken to be time along the ray, then
 equals the propagation velocity v.
equals the propagation velocity v.





Next: One-way wave-equation
Up: Riemannian wavefield extrapolation
Previous: Introduction
Stanford Exploration Project
11/4/2004
![]() in an arbitrary Riemannian space with coordinates
in an arbitrary Riemannian space with coordinates
![]() takes the form
takes the form
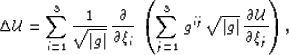
![]() ,is orthogonal to the other coordinates
,is orthogonal to the other coordinates ![]() .
The metric tensor reduces to
.
The metric tensor reduces to
![\begin{displaymath}
\left[g_{ij}\right] = \lb\bea{ccc}
E& F& 0 \\ F& G& 0 \\ 0 & 0 & \AA^2
\eea\rb\;,\end{displaymath}](img10.gif)
![]() has the matrix
has the matrix
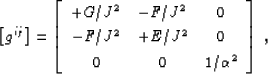
![]() ,
, ![]() , and
, and ![]() ,
with
,
with ![]() orthogonal to both
orthogonal to both ![]() and
and ![]() ,we obtain the Helmholtz wave helm
for propagating waves in a 3D semi-orthogonal Riemannian space:
1ÅJ
,we obtain the Helmholtz wave helm
for propagating waves in a 3D semi-orthogonal Riemannian space:
1ÅJ
![]() is the wave propagation velocity mapped to Riemannian coordinates.
is the wave propagation velocity mapped to Riemannian coordinates.