Introduction

Imaging complex geology is one of the main challenges of today's seismic processing. Of the many seismic imaging methods available, downward continuation (24) is accurate, robust, and capable of handling models with large and sharp velocity variations. This method naturally handles the multipathing that occurs in complex geology and provide a band-limited solution to the seismic imaging problem. Furthermore, as computational power increases, such methods are gradually moving into the mainstream of seismic processing. This explains why one-way wave extrapolation has been a subject of extensive theoretical research in the recent years (110; 49; 51; 7; 81).

However, migration by downward continuation imposes strong limitations on the dip of reflectors that can be imaged since, by design, it favors downward propagating energy. Upward propagating energy, for example overturning waves, can be imaged in principle using downward continuation methods (42), although the procedure is difficult, particularly for prestack data. In contrast, Kirchhoff-type methods based on ray-traced traveltimes can image steep dips and handle overturning waves, although those methods are far less reliable in complex velocity models given their asymptotic assumption (40).

The steep-dip limitation of downward continuation techniques has been addressed in several ways:

A first option is to increase the angular accuracy of the extrapolation operator, for example by employing methods from the Fourier finite-difference (FFD) family (7; 81), or the Generalized Screen Propagator (GSP) family (49; 51). The enhancements brought about by these methods have two costs: (1) they increase the cost of extrapolation, and (2) they do not guarantee unconditional stability. A second option is to perform the wavefield extrapolation in tilted coordinate systems (34), or by designing sources that favor illumination of particular regions of the image (21; 80). We can thus increase angular accuracy, although these methods are best suited for only a subset of the model (a salt flank, for example), and potentially decrease the accuracy in other regions of the model. In complex geology, defining an optimal tilt angle for the extrapolation grid is not obvious. A third possibility is hybridization of wavefield and ray-based techniques, either in the form of Gaussian beams (19; 39; 46; 47), coherent states (4; 5), or beam-waves (15). Such techniques are quite powerful, since they couple wavefield methods with multipathing and band-limited properties, with ray methods, which deliver arbitrary directions of propagation, even overturning. Beams can be understood as localized wave packets propagating in the preferential direction (117). Numerically, they are usually implemented using localized extrapolation paths. Extrapolation beams may leave shadow zones in various parts of the model, which hamper their imaging abilities. Furthermore, extrapolation beams have limited width, and do not allow diffractions from sharp features in the velocity model to develop completely without being attenuated at the boundaries. In addition, the narrow extrapolation domain generates beam superposition artifacts, such as beam boundary effects.

We can recognize that Cartesian coordinates for downward and tilted continuation or along beams of limited spatial extent, are just mathematical conveniences that do not reflect a physical reality. A better idea is to reformulate wavefield extrapolation in general Riemannian coordinates that conform with the general direction of wave propagation, thus the name Riemannian wavefield extrapolation (RWE). We can formulate the wavefield extrapolation theory in arbitrary 3D semi-orthogonal Riemannian spaces (79), where the extrapolation direction is orthogonal to all other directions. Examples of such coordinate systems include, but are not limited to, fans of rays emerging from a source point, or bundles of rays initiated by plane waves of arbitrary initial dips at the source. For constant background velocity, this method reduces to extrapolation in polar/spherical coordinates (64; 65), or extrapolation in tilted coordinates (34). This method is also closely related to Huygens wavefront tracing (92), which represents a finite-difference solution to the eikonal equation in ray coordinates.

The main strength of this method is that the coordinate system can follow the waves, which may overturn, such that we can use one-way extrapolators to image diving waves (overturned).

 

overturned
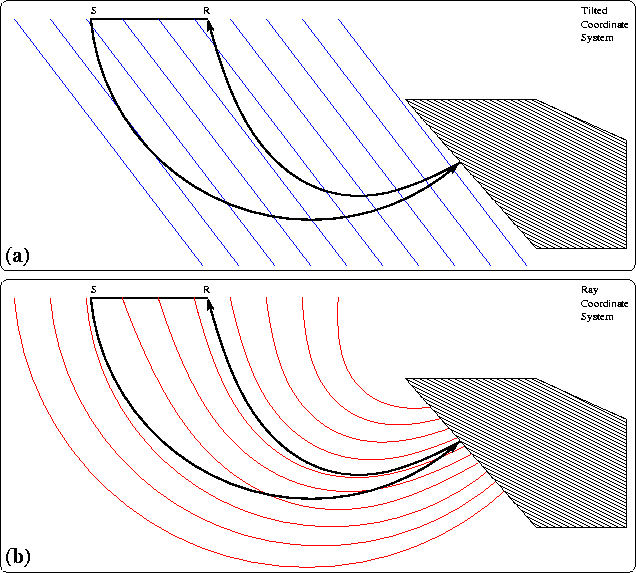
Figure 1 Ray coordinate systems are superior to tilted coordinate systems for imaging overturning waves using one-way wavefield extrapolators. Overturning reflected energy may become evanescent in tilted coordinate systems (a), but stays non-evanescent in ray coordinate systems (b).

We can also use inexpensive extrapolators with limited angle accuracy (e.g. $15^\circ$), since, in principle, we are never too far from the wave propagation direction, and those methods deliver unconditional stability. We are also not confined to the extent of any individual extrapolation beam, therefore we can track diffractions for their entire spatial extent (beams).

 

beams
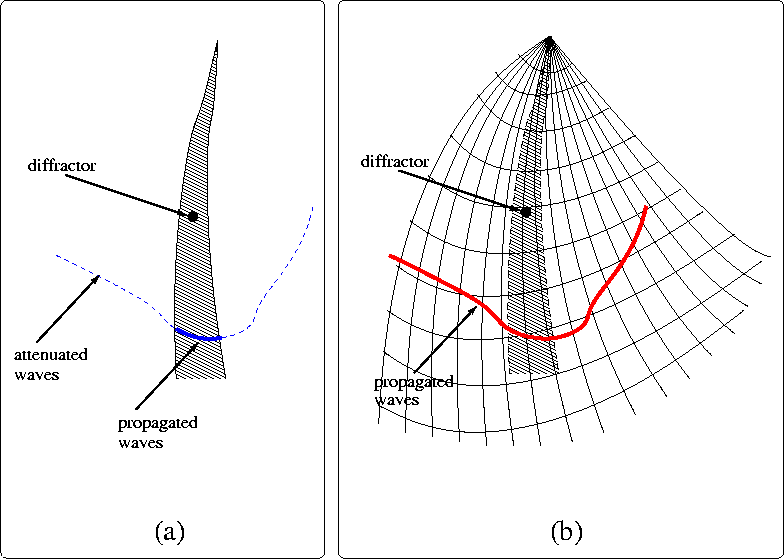
Figure 2 Extrapolated energy is attenuated at beam boundaries (a), but is propagated in a Riemmanian coordinate system (b).