




Next: References
Up: Berryman: Bounds on geomechanical
Previous: APPENDIX A: Peselnick-Meister-Watt Bounds
One of the bounds of Dederichs and Zeller (1973) is based
on the assumption that, inside each grain of a multiphase material,
the distribution of different phases is independent of the shape
of the grain, and also independent of the phases of contiguous grains.
Grains are therefore assumed to be completely uncorrelated, both
internally and externally. The results obtained for bulk modulus are:
| ![\begin{displaymath}
K_{DZ}^\pm = \left[\sum_{n=1}^N \frac{f_n}{K_n +4g_\pm/3}\right]^{-1}
- 4g_\pm/3,
\end{displaymath}](img80.gif) |
(26) |
where
| 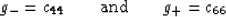 |
(27) |
in our present notation [see eq. (7)].
Similarly, for shear modulus, we have
| ![\begin{displaymath}
\mu_{DZ}^\pm = \left[\sum_{n=1}^N \frac{f_n}{\mu_n +\zeta_\pm}\right]^{-1}
- \zeta_\pm,
\end{displaymath}](img82.gif) |
(28) |
where
| 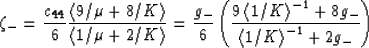 |
(29) |
and
| 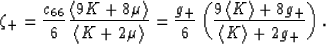 |
(30) |
These bounds on bulk modulus are the same as those of Beran and
Molyneux (1966) and Miller (1969). The upper bound on shear
modulus is the same as that of McCoy (1970) and Silnutzer (1972).
Because of the simple functional form of both sets
of bounds, it is easy to show (Berryman, 1982) that they are always
at least as restrictive as -- and, for nonnegligible volume
fractions of inclusions, normally a significant improvement upon --
the Hashin-Shtrikman bounds (Hashin and Shtrikman, 1962; 1963).
We chose to consider these bounds here because they depend only on simple
volume averages of the constituent elastic constants, and also because
they show -- by way of contrast to the other bounds (see Figures 1 and 2) --
that it does indeed matter what
assumptions are made about the microstructure of the composite.





Next: References
Up: Berryman: Bounds on geomechanical
Previous: APPENDIX A: Peselnick-Meister-Watt Bounds
Stanford Exploration Project
10/23/2004
![\begin{displaymath}
K_{DZ}^\pm = \left[\sum_{n=1}^N \frac{f_n}{K_n +4g_\pm/3}\right]^{-1}
- 4g_\pm/3,
\end{displaymath}](img80.gif)
![\begin{displaymath}
K_{DZ}^\pm = \left[\sum_{n=1}^N \frac{f_n}{K_n +4g_\pm/3}\right]^{-1}
- 4g_\pm/3,
\end{displaymath}](img80.gif)
![\begin{displaymath}
\mu_{DZ}^\pm = \left[\sum_{n=1}^N \frac{f_n}{\mu_n +\zeta_\pm}\right]^{-1}
- \zeta_\pm,
\end{displaymath}](img82.gif)