Since accurate imaging of reflectors is more important in the neighborhood of the reservoir, it makes sense to apply a target-oriented strategy to reduce the number of depth steps. A way to achieve this objective is to write the modeling operator ![]() in a target-oriented fashion and explicitly compute the Hessian.
in a target-oriented fashion and explicitly compute the Hessian.
In general, the synthetic data for one frequency, a shot positioned at ![]() and a receiver positioned at
and a receiver positioned at ![]() can be given by a linear operator
can be given by a linear operator ![]() acting on the full model space
acting on the full model space ![]() with
with ![]() (
(![]() in 2D ) as
in 2D ) as
| |
(4) |
In equation (4), two important properties have been used Ehinger et al. (1996): first, the Green functions are computed by means of the one-way wave equation, and second, the extrapolation is performed by using the adequate paraxial wave equations (flux conservation) Bamberger et al. (1988).
The quadratic cost function is
| (5) |
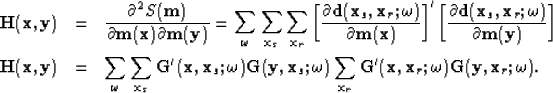 |
(6) | |
| (7) |
| (8) |
In the next section we show three numerical examples of Hessians estimated with the proposed target-oriented approach.