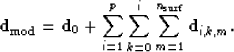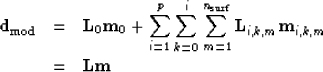Next: LSJIMP: Least-squares minimization
Up: 2-D Theory \label>chapter:theory2d>
Previous: 2-D Theory \label>chapter:theory2d>
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) motivates LSJIMP. The Figure assumes that the
recorded data is the superposition of primary events and pegleg multiples from
the seabed. In effect, the images constructed from the primaries and from each
mode of multiple constitute independent measurements of the earth's reflectivity
at depth. Unfortunately, these independent measurements are embedded in a single
data record. We would like to improve signal-to-noise ratio or fill illumination
gaps by averaging the images. However, simple averaging of the raw images
encounters two problems. First, unless the multiple images have undergone an
appropriate amplitude correction, the signal events are incommensurable.
Secondly, corresponding crosstalk events on the primary and multiple images are
kinematically quite consistent, especially at near offsets, meaning that
averaging the images will do little to increase the signal-to-noise ratio or
signal fidelity.
motivates LSJIMP. The Figure assumes that the
recorded data is the superposition of primary events and pegleg multiples from
the seabed. In effect, the images constructed from the primaries and from each
mode of multiple constitute independent measurements of the earth's reflectivity
at depth. Unfortunately, these independent measurements are embedded in a single
data record. We would like to improve signal-to-noise ratio or fill illumination
gaps by averaging the images. However, simple averaging of the raw images
encounters two problems. First, unless the multiple images have undergone an
appropriate amplitude correction, the signal events are incommensurable.
Secondly, corresponding crosstalk events on the primary and multiple images are
kinematically quite consistent, especially at near offsets, meaning that
averaging the images will do little to increase the signal-to-noise ratio or
signal fidelity.
The previous paragraph underscores the main obstacle facing algorithms which
attempt to jointly image multiples and primaries: while multiples provide
additional information about the earth's reflectivity, we cannot exploit it
unless we separate the individual modes. Cleanly separating a variety of
different multiple modes from prestack data is both expensive and difficult.
Moreover, by casting mode separation as a preprocessing step, as is the norm, we
risk biasing the amplitudes in the separated modes, which could inhibit the
integration.
LSJIMP solves the separation and integration problems simultaneously, as a global
least-squares inversion problem. The model space, as illustrated in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , contains a collection of images, with the energy from
each mode partitioned into one, and only one image. Moreover, each image has a
special form: because the forward modeling operator contains appropriate
amplitude correction operators the signal events in multiple and primary images
are directly comparable, in terms of both kinematics and amplitudes. In order
to solve the integration problem, we can apply a model regularization operator
which penalizes inconsistency between images, and thus ``spreads'' signal from
one model panel to another, using the multiples to fill gaps in the primary
illumination and to increase signal fidelity.
, contains a collection of images, with the energy from
each mode partitioned into one, and only one image. Moreover, each image has a
special form: because the forward modeling operator contains appropriate
amplitude correction operators the signal events in multiple and primary images
are directly comparable, in terms of both kinematics and amplitudes. In order
to solve the integration problem, we can apply a model regularization operator
which penalizes inconsistency between images, and thus ``spreads'' signal from
one model panel to another, using the multiples to fill gaps in the primary
illumination and to increase signal fidelity.
LSJIMP models the recorded data as the superposition of primary reflections and
p orders of pegleg multiples from 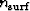 multiple-generating surfaces.
An
multiple-generating surfaces.
An 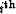 order pegleg splits into i+1 legs. If we denote the primaries
as
order pegleg splits into i+1 legs. If we denote the primaries
as 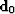 and the
and the 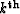 leg of the
leg of the 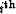 order pegleg from the
order pegleg from the
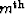 multiple generator as
multiple generator as 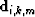 , the modeled data takes the
following form:
, the modeled data takes the
following form:
| 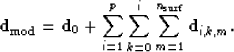 |
(1) |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates a simple case, where we model only
first-order peglegs from a the seabed (
illustrates a simple case, where we model only
first-order peglegs from a the seabed (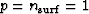 ).
).
Other authors have solved a similar least-squares problem.
() jointly imaged and separated compressional waves and
various (non-multiple) embedded coherent noise modes.
() used nonstationary prediction-error filters to model
primaries and surface-related multiples, but cast the problem purely in terms of
wavefield separation, rather than joint imaging of multiples and primaries.
If we have designed an imaging operator that produces primary and multiple images
with consistent signal (kinematics and angle-dependent amplitudes), then we
assume that we can model the important events in the data. Let us denote the
modeling operator (adjoint to imaging) for primaries  and the image of
the primaries
and the image of
the primaries 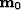 . Similarly, for the
. Similarly, for the 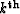 leg of the
leg of the
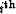 order pegleg from the
order pegleg from the 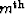 multiple generator, we denote the
modeling operator and image
multiple generator, we denote the
modeling operator and image 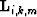 and
and 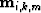 ,
respectively. Following Figure
,
respectively. Following Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we can rewrite equation
(1):
, we can rewrite equation
(1):
| 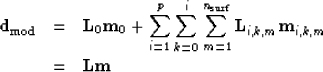 |
(2) |
| (3) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , contains a collection of images, with the energy from
each mode partitioned into one, and only one image. Moreover, each image has a
special form: because the forward modeling operator contains appropriate
amplitude correction operators the signal events in multiple and primary images
are directly comparable, in terms of both kinematics and amplitudes. In order
to solve the integration problem, we can apply a model regularization operator
which penalizes inconsistency between images, and thus ``spreads'' signal from
one model panel to another, using the multiples to fill gaps in the primary
illumination and to increase signal fidelity.
, contains a collection of images, with the energy from
each mode partitioned into one, and only one image. Moreover, each image has a
special form: because the forward modeling operator contains appropriate
amplitude correction operators the signal events in multiple and primary images
are directly comparable, in terms of both kinematics and amplitudes. In order
to solve the integration problem, we can apply a model regularization operator
which penalizes inconsistency between images, and thus ``spreads'' signal from
one model panel to another, using the multiples to fill gaps in the primary
illumination and to increase signal fidelity.