




Next: Amplitude corrections for pegleg
Up: Particular Implementation of LSJIMP
Previous: Particular Implementation of LSJIMP
Kinematic imaging of pegleg multiples in a laterally-homogeneous earth
In a ``1-D Earth'' (horizontally-stratified, v(z) medium), the normal-moveout
(NMO) equation () describes the prestack traveltime curve
of a primary reflection at relatively short source-receiver offset:
| 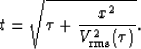 |
(16) |
Applied as an offset-dependent vertical time shift to a CMP gather, the NMO
equation flattens an arbitrary primary to its zero-offset traveltime  ,
where (half) offset is denoted x and the root-mean-square (RMS) velocity,
,
where (half) offset is denoted x and the root-mean-square (RMS) velocity,
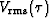 , is defined in a laterally-homogeneous earth as:
, is defined in a laterally-homogeneous earth as:
| 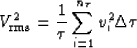 |
(17) |
The earth is parameterized by 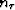 layers of time thickness
layers of time thickness 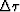 ,
with constant interval velocity vi in each layer.
,
with constant interval velocity vi in each layer.
Analogously, a modified NMO equation can image pegleg multiples in a 1-D Earth,
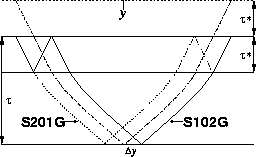
as motivated graphically by Figure 3. From the figure, we see that
kinematically, a first-order pegleg can be conceptualized as a ``pseudo-primary''
with the same offset, but with an additional two-way zero-offset traveltime to
the multiple generator, 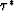 . In equation form, let us extend this intuition
to the general case of a
. In equation form, let us extend this intuition
to the general case of a 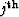 -order pegleg to write an NMO equation for
peglegs:
-order pegleg to write an NMO equation for
peglegs:
| 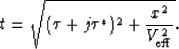 |
(18) |
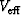 is the effective RMS velocity of the pseudo-primary shown in Figure
3. To derive an expression for
is the effective RMS velocity of the pseudo-primary shown in Figure
3. To derive an expression for 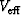 , we modify the
definition of RMS velocity, equation (17), to reflect a
, we modify the
definition of RMS velocity, equation (17), to reflect a
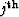 -order pegleg multiple's additional travel between the surface and
multiple generator:
-order pegleg multiple's additional travel between the surface and
multiple generator:
| 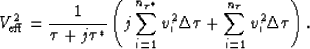 |
(19) |
Analogously, 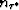 is the number of assumed layers between the earth's
surface and the multiple generator. Notice that the two terms inside the
parentheses of equation (19) are simply the definition of RMS
velocity at
is the number of assumed layers between the earth's
surface and the multiple generator. Notice that the two terms inside the
parentheses of equation (19) are simply the definition of RMS
velocity at 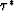 and
and  , respectively. We can substitute equation
(19) accordingly to derive the final expression for
, respectively. We can substitute equation
(19) accordingly to derive the final expression for 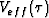 :
:
| 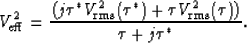 |
(20) |
() derives a similar series of expressions.
schem
Figure 3 Pegleg multiples ``S201G'' and ``S102G'' have the
same traveltimes as ``pseudo-primary'' with the same offset and an extra
zero-offset traveltime 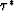 . . |
|  |






Next: Amplitude corrections for pegleg
Up: Particular Implementation of LSJIMP
Previous: Particular Implementation of LSJIMP
Stanford Exploration Project
5/30/2004
![]() . In equation form, let us extend this intuition
to the general case of a
. In equation form, let us extend this intuition
to the general case of a ![]() -order pegleg to write an NMO equation for
peglegs:
-order pegleg to write an NMO equation for
peglegs:
