Next: Thesis Outline
Up: Least-squares joint imaging of
Previous: Least-squares joint imaging of
Introduction
Prospecting by the seismic reflection method has revolutionized hydrocarbon
exploration. Accurate 3-D reflection seismic imaging of complex structures
(along with horizontal drilling) has increased success rates to the point where
exploration and production in thousands of feet of water is now often
economically feasible. This success, however, appears to fly in the face of
common sense. Despite an inherently noisy earth, weak reflected signal, deep
reservoirs, and a complex wavefield, seismic images constructed with
singly-reflected P-waves (henceforth, ``primary reflections'' or ``primaries'')
alone often suffice to plan drilling activities.
Modern marine seismic acquisition generally yields higher quality recorded data
than terrestrial acquisition. Marine towed-streamer surveys sample the wavefield
densely, regularly, and at a relatively low cost. Marine data is immune from a
variety of factors which combine to degrade terrestrial data quality: a non-flat
acquisition datum, near-surface inhomogeneity, and strong surface waves.
However, the water column's relative homogeneity and the near-perfect
reflectivity at the water's surface almost always produce observable
multiply-reflected P-waves (henceforth, ``multiple reflections'' or
``multiples''). Multiples often erect the most significant impediment to the
successful construction and interpretation of an image of the primaries,
especially in regions with anomalously strong reflectors (e.g., ``hard'' water
bottom or salt bodies). Multiple suppression techniques have, by necessity,
advanced contemporaneously with reflection imaging for fifty years.
Despite its nuisance, however, energy from multiples penetrates deeply enough
into the earth to illuminate the prospect zone. In this sense, the multiples can
be viewed as perfectly viable signal, rather than as noise. Moreover, since they
illuminate different angular ranges and reflection points, a primary and its
multiples are more than simply redundant. In theory and in practice, multiples
provide subsurface information not found in the primaries.
To actually exploit the information provided by multiples, the multiples and
primaries must first be mapped into a domain where they are directly comparable,
and then combined in some fashion. Imaging algorithms like migration reduce the
signal to a compact form by removing the effects of wave propagation through a
the overburden. Additionally, if the prestack images are arranged in
angle-domain common-image gathers (see Sava and Fomel (2003) for a review),
the events can be analyzed for angle-dependent phenomenon. We conclude,
therefore that the prestack image domain, and in particular, the angle domain, is
the best one in which to integrate the information contained in the multiples and
primaries.
An important class of multiple suppression techniques create from the data a
``model'' of the multiples, which may then be adaptively subtracted from the
data. Many of these algorithms use wavefield extrapolation to ``add a multiple
bounce'' to recorded data, and thus transform primaries into an estimate of the
multiples
Berryhill and Kim (1986); Lu et al. (1999); Morley (1982); Riley and Claerbout (1976); Tsai (1985); Verschuur et al. (1992); Wiggins (1988).
The imaging of multiples can be viewed roughly as the reverse process of modeling.
Prestack imaging of multiples ``removes a multiple bounce'' from the data and
transforms multiples into pseudo-primary events Berkhout and Verschuur (2003); Shan (2003)
which can then be imaged using conventional imaging techniques.
Existing migration techniques for multiples perform the reverse modeling process
either implicitly or explicitly. Reiter et al. (1991) imaged pegleg
multiples with Kirchhoff prestack depth migration. He and Schuster (2003)
present a least-squares joint imaging scheme for multiples that uses poststack
Kirchhoff depth migration. Yu and Schuster (2001) and
Guitton (2002) migrate peglegs with shot-profile depth migration,
while Berkhout and Verschuur (1994) used a similar crosscorrelation technique.
Shan (2003) uses source-geophone migration after crosscorrelation at the
surface. In many ways, however, these techniques fail to fully leverage the
valuable information contained in the multiples.
In effect, primaries and each mode of multiple constitute semi-independent
measurements of the earth's reflectivity at depth. Unfortunately, these
independent measurements are embedded in a single data record. We would like to
improve signal-to-noise ratio or fill illumination gaps by averaging the images.
However, simple averaging of the raw images
Berkhout and Verschuur (1994); Reiter et al. (1991); Shan (2003) encounters two problems, illustrated
by Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . First, unless the
multiple images have undergone an appropriate amplitude correction, the signal
events are incommensurable. Secondly, just as multiples constitute noise on the
primary image, primaries and higher order multiples constitute noise on the
first-order multiple image. The unmodeled events on each image are called
``crosstalk'' Claerbout (1992). Because corresponding crosstalk
events on the primary and multiple images are kinematically quite consistent,
especially at near offsets, averaging the images may not increase the
signal-to-noise ratio or improve signal fidelity.
. First, unless the
multiple images have undergone an appropriate amplitude correction, the signal
events are incommensurable. Secondly, just as multiples constitute noise on the
primary image, primaries and higher order multiples constitute noise on the
first-order multiple image. The unmodeled events on each image are called
``crosstalk'' Claerbout (1992). Because corresponding crosstalk
events on the primary and multiple images are kinematically quite consistent,
especially at near offsets, averaging the images may not increase the
signal-to-noise ratio or improve signal fidelity.
gulf-schem
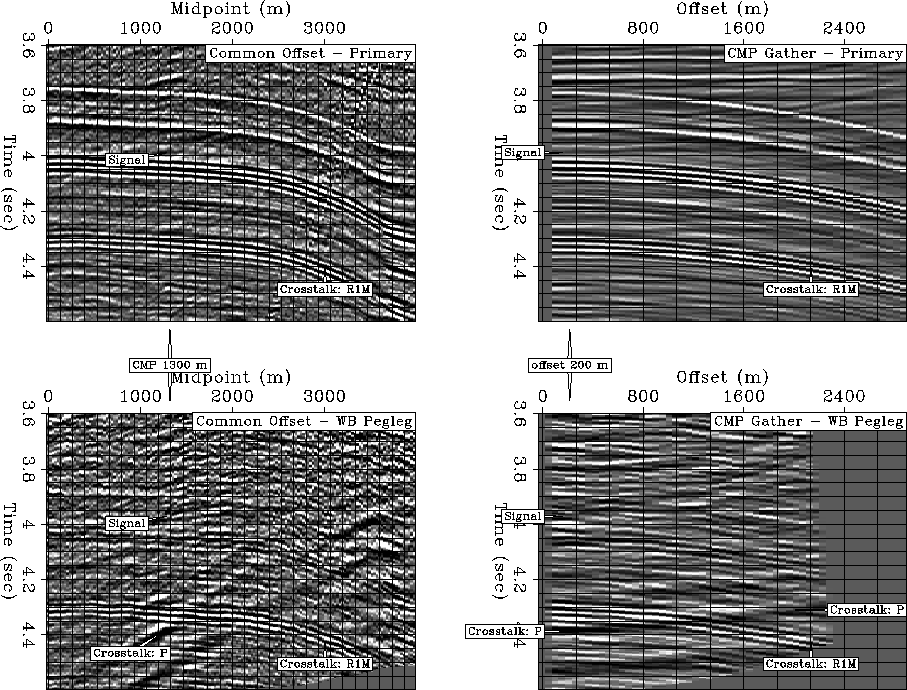
Figure 1 Common-offset section and common-midpoint (CMP)
gather from 2-D field data example after normal moveout (NMO) for primaries
(left panels) and a particular prestack, true relative amplitude imaging method
for pegleg multiples (Section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Signal events are
consistent between all panels, both kinematically and in terms of amplitudes.
The multiples provide near offset information not found in the primaries.
However, the multiple image contains crosstalk events - overcorrected
primaries (``P'') and multiples from other reflectors (``R1M'') - that
inhibit simple averaging of the multiple and primary images. The crosstalk
events shown here are, however, inconsistent between images, and to some extent
curved with respect to offset, and can thus be distinguished from signal
events, which are both flat and consistent between images.
). Signal events are
consistent between all panels, both kinematically and in terms of amplitudes.
The multiples provide near offset information not found in the primaries.
However, the multiple image contains crosstalk events - overcorrected
primaries (``P'') and multiples from other reflectors (``R1M'') - that
inhibit simple averaging of the multiple and primary images. The crosstalk
events shown here are, however, inconsistent between images, and to some extent
curved with respect to offset, and can thus be distinguished from signal
events, which are both flat and consistent between images.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





gulf-schem-deep
Figure 2 Same format as Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
but taken from deeper in the section, after the arrival of the first seabed
multiple. Weak signal events are visible on both images, but corresponding
crosstalk events (e.g., ``R1M'') are generally consistent between images and
would greatly inhibit the effectiveness of simple image averaging. However,
they are curved with respect to offset, while signal events are flat.
,
but taken from deeper in the section, after the arrival of the first seabed
multiple. Weak signal events are visible on both images, but corresponding
crosstalk events (e.g., ``R1M'') are generally consistent between images and
would greatly inhibit the effectiveness of simple image averaging. However,
they are curved with respect to offset, while signal events are flat.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





The previous paragraph underscores the main obstacle facing algorithms which
attempt to jointly image multiples and primaries: while multiples provide
additional information about the earth's reflectivity, we cannot exploit it
unless we separate the individual modes. Cleanly separating a variety of
different multiple modes from prestack data is both expensive and difficult.
Moreover, by casting mode separation as a preprocessing step, as is the norm, we
may bias the amplitudes in the separated modes and thus inhibit the integration
of primaries and multiples.
In this thesis I introduce the LSJIMP (Least-squares Joint Imaging of Multiples
and Primaries) method, which solves the separation and integration problems
simultaneously, as a global least-squares inversion problem. The model space of
the inverse problem, as illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , contains
a collection of images, with the energy from each mode partitioned into one, and
only one image. Moreover, each image has a special form: because the forward
modeling operator contains appropriate amplitude correction operators, the signal
events in multiple and primary images are directly comparable, in terms of both
kinematics and amplitudes.
, contains
a collection of images, with the energy from each mode partitioned into one, and
only one image. Moreover, each image has a special form: because the forward
modeling operator contains appropriate amplitude correction operators, the signal
events in multiple and primary images are directly comparable, in terms of both
kinematics and amplitudes.
Minimization of the modeling error (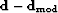 in Figure
in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) alone is an ill-posed problem. Forward-modeled
crosstalk is indistinguishable from forward-modeled signal. I devise three model
regularization operators which discriminate between crosstalk and signal and
thereby properly segregate energy from each modeled wave mode into its respective
image. Figure
) alone is an ill-posed problem. Forward-modeled
crosstalk is indistinguishable from forward-modeled signal. I devise three model
regularization operators which discriminate between crosstalk and signal and
thereby properly segregate energy from each modeled wave mode into its respective
image. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates these discriminants on
a field data example. The model regularization operators serve a higher purpose
than crosstalk suppression alone, however. By applying differential operators
along reflection angle and between images, we can ``spread'' signal from other
angles or images to fill illumination gaps and increase signal fidelity.
Furthermore, by exploiting an additional, and hitherto ignored dimension of data
redundancy - that between primaries and multiples - we can, with a degree of
rigor, solve the integration problem and rightly claim to have solved a ``joint
imaging'' problem.
illustrates these discriminants on
a field data example. The model regularization operators serve a higher purpose
than crosstalk suppression alone, however. By applying differential operators
along reflection angle and between images, we can ``spread'' signal from other
angles or images to fill illumination gaps and increase signal fidelity.
Furthermore, by exploiting an additional, and hitherto ignored dimension of data
redundancy - that between primaries and multiples - we can, with a degree of
rigor, solve the integration problem and rightly claim to have solved a ``joint
imaging'' problem.
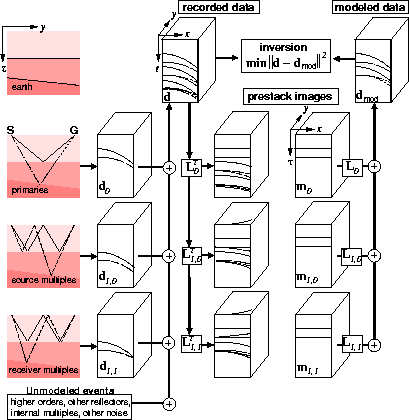
schem-LSJIMP-seg
Figure 3 LSJIMP schematic. Assume that the recorded
data consist of primaries and pegleg multiples. Prestack imaging alone
(applying adjoint of modeling operator 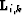 ) focuses signal events
in zero-offset traveltime (or depth) and offset (or reflection angle), but
leaves behind crosstalk events. If the
) focuses signal events
in zero-offset traveltime (or depth) and offset (or reflection angle), but
leaves behind crosstalk events. If the 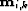 images contain only
signal, then we can model all the events in the data that we desire. The
LSJIMP inversion suppresses crosstalk and endeavors to fit the recorded data in
a least-squares sense. The model regularization operators used to suppress
crosstalk simultaneously enable LSJIMP to exploit the intrinsic redundancy
between and within the images to increase signal fidelity.
images contain only
signal, then we can model all the events in the data that we desire. The
LSJIMP inversion suppresses crosstalk and endeavors to fit the recorded data in
a least-squares sense. The model regularization operators used to suppress
crosstalk simultaneously enable LSJIMP to exploit the intrinsic redundancy
between and within the images to increase signal fidelity.

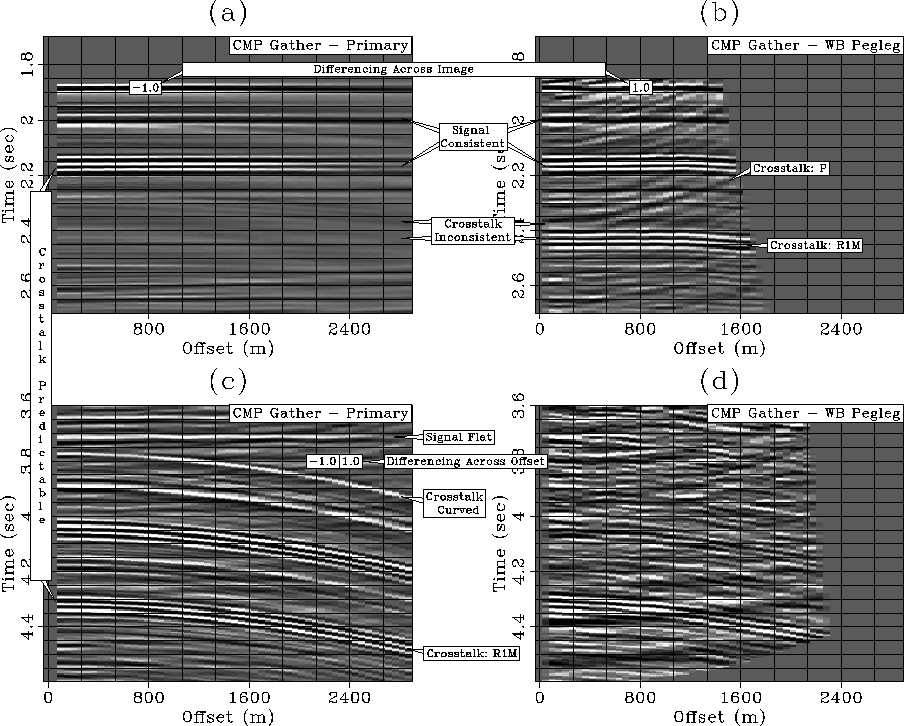
gulf-schem-redun-geo
Figure 4 Illustration of intrinsic redundancy
within and between prestack images of primaries (panels (a) and (c)) and
peglegs (panels (b) and (d)), and the regularization schemes used by LSJIMP to
exploit this redundancy to suppress crosstalk, increase signal fidelity, and
fill illumination gaps. All panels are CMP gathers from the same midpoint, but
the upper and lower panels zoom into small portions of the time axis for
viewing purposes. Between panels (a) and (b), notice how signal events are
consistent (kinematics and amplitudes) between images, while crosstalk events
are not. A differencing operator between images increases signal consistency
and penalizes crosstalk. On panel (c), notice that signal events are flat with
offset, while crosstalk events are generally curved. Differencing between
adjacent offsets increases signal fidelity and suppresses crosstalk. Lastly,
from panels (a) and (c), notice how we can use signal to predict crosstalk
events. The predicted crosstalk can be used as a model penalty weight which
penalizes crosstalk.










Next: Thesis Outline
Up: Least-squares joint imaging of
Previous: Least-squares joint imaging of
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . First, unless the
multiple images have undergone an appropriate amplitude correction, the signal
events are incommensurable. Secondly, just as multiples constitute noise on the
primary image, primaries and higher order multiples constitute noise on the
first-order multiple image. The unmodeled events on each image are called
``crosstalk'' Claerbout (1992). Because corresponding crosstalk
events on the primary and multiple images are kinematically quite consistent,
especially at near offsets, averaging the images may not increase the
signal-to-noise ratio or improve signal fidelity.
. First, unless the
multiple images have undergone an appropriate amplitude correction, the signal
events are incommensurable. Secondly, just as multiples constitute noise on the
primary image, primaries and higher order multiples constitute noise on the
first-order multiple image. The unmodeled events on each image are called
``crosstalk'' Claerbout (1992). Because corresponding crosstalk
events on the primary and multiple images are kinematically quite consistent,
especially at near offsets, averaging the images may not increase the
signal-to-noise ratio or improve signal fidelity.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)