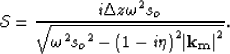Next: The boundary condition correction
Up: Application to linearized downward
Previous: Application to linearized downward
Let us define a slowness perturbation 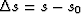 as a difference
between two slowness models, one of which (s0) is named the
``background slowness''. By undertaking several approximations, the
most notable of which is Born, the mixed-domain downward continuation
operator can be written as an explicit function of the slowness
perturbation. This allows an explicit relation between the slowness
perturbation and the wavefield. In conjunction with the imaging
condition, this allows writing an explicit relation between the slowness
perturbation and the image. This relation is
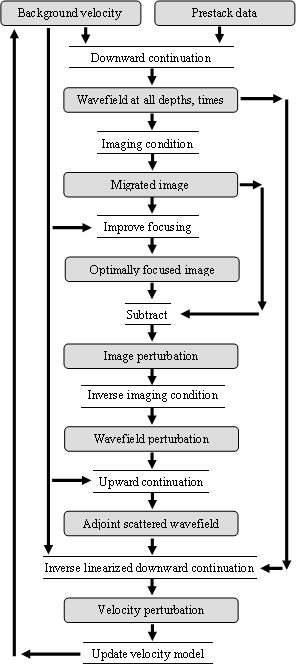
the basis of Wave-Equation Migration Velocity Analysis (WEMVA), a
complete flowchart of which is presented in Figure 3.
This
procedure finds the velocities in the following way: using the
recorded data and the background slowness, it creates a background
image. This image is then improved so that it is closer to the
optimally focused one, then the two images are subtracted to create an
image perturbation. This is transformed into a wavefield perturbation
through an inverse imaging condition, then is upward continued, to
create an adjoint scattered wavefield. This in turn is transformed
into a slowness update by inverting the linearized downward
continuation operator. This operator is linearized so that its
inversion will be computationally cheap. A complete derivation is
provided by Biondi and Sava (1999), with more explanations
in Sava (2000).
as a difference
between two slowness models, one of which (s0) is named the
``background slowness''. By undertaking several approximations, the
most notable of which is Born, the mixed-domain downward continuation
operator can be written as an explicit function of the slowness
perturbation. This allows an explicit relation between the slowness
perturbation and the wavefield. In conjunction with the imaging
condition, this allows writing an explicit relation between the slowness
perturbation and the image. This relation is
the basis of Wave-Equation Migration Velocity Analysis (WEMVA), a
complete flowchart of which is presented in Figure 3.
This
procedure finds the velocities in the following way: using the
recorded data and the background slowness, it creates a background
image. This image is then improved so that it is closer to the
optimally focused one, then the two images are subtracted to create an
image perturbation. This is transformed into a wavefield perturbation
through an inverse imaging condition, then is upward continued, to
create an adjoint scattered wavefield. This in turn is transformed
into a slowness update by inverting the linearized downward
continuation operator. This operator is linearized so that its
inversion will be computationally cheap. A complete derivation is
provided by Biondi and Sava (1999), with more explanations
in Sava (2000).
wemva
Figure 3 WEMVA flowchart, provided for illustrating the
use of linearized downward continuation.
|
|  |

If we denote the wavefield as U, the linearized downward
continuation (complexified local Born-Fourier method), according to Appendix B in Vlad (2002), is given by:
| ![\begin{displaymath}
U_{z = n\Delta z} = \left( {\prod\limits_1^n {\mathcal T} }
...
...( {\prod\limits_1^j {\mathcal T} } \right)U_{z = 0} } \right]},\end{displaymath}](img3.gif) |
(2) |
where 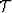 is the background wavefield downward continuation
operator:
is the background wavefield downward continuation
operator:
| 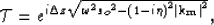 |
(3) |
and 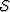 is the scattering operator:
is the scattering operator:
| 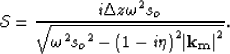 |
(4) |





Next: The boundary condition correction
Up: Application to linearized downward
Previous: Application to linearized downward
Stanford Exploration Project
5/23/2004


![\begin{displaymath}
U_{z = n\Delta z} = \left( {\prod\limits_1^n {\mathcal T} }
...
...( {\prod\limits_1^j {\mathcal T} } \right)U_{z = 0} } \right]},\end{displaymath}](img3.gif)