Iteratively Reweighted Least Squares (IRLS)

Instead of L²-norm solutions obtained by the conventional LS solution, L^p-norm minimization solutions, with $1\le p \le2$, are often tried. Iterative inversion algorithms called IRLS (Iteratively Reweighted Least Squares) algorithms have been developed to solve these problems, which lie between the least-absolute-values problem and the classical least-squares problem. The main advantage of IRLS is to provide an easy way to compute the approximate L¹-norm solution. L¹-norm solutions are known to be more robust than L²-norm solutions, being less sensitive to spiky, high-amplitude noise Claerbout and Muir (1973); Scales et al. (1988); Scales and Gersztenkorn (1987); Taylor et al. (1979).

The problem solved by IRLS is a minimization of the weighted residual in the least-squares sense :

$$\bold r = \bold W (\bold L\bold m - \bold d) .$$ (5)

The gradient for the weighted residual in the least-squares sense becomes

$$\bold L^T \bold W \bold r = {\partial \over \partial \bold ... ...L\bold m -\bold d)^T\bold W^T\bold W(\bold L\bold m -\bold d) .$$ (6)

The particular choice for $\bold W$ is the one that results in minimizing the L^p norm of the residual. Choosing the i^th diagonal element of $\bold W$ to be a function of the i^th component of the residual vector as follows:

$$\mbox {diag} (\bold W)= \vert\bold r\vert^{(p-2)/2} ,$$ (7)

the norm of the weighted residual is then

$$\bold r^T \bold W^T \bold W \bold r = \bold r^T \vert\bold r\vert^{(p-2)} \bold r = \vert\bold r\vert^p .$$ (8)

Therefore, this can be thought of as a method that estimates the gradient in the L^p-norm of the residual. This method is valid for norms where $1\le p \le2$. When the L¹-norm is desired, the weighting is as follows:

$$\mbox {diag} (\bold W) = \vert\bold r\vert^{-1/2}.$$

This will reduce the contribution of large residuals and improve the fit to the data that is already well-estimated. Thus, the L¹-norm-based minimization is robust, less sensitive to noise bursts in the data. Huber proposed a hybrid L¹/L²-norm Huber (1973) that treats the small residuals in an L²-norm sense and the large residuals in an L¹-norm sense. This approach deals with both bursty and Gaussian-type noise, and can be realized by weighting as follows:

$$\mbox{diag} (\bold W) = \left\{ \begin{array} {cc} \vert\bol... ...on \\ 1, & \vert\bold r\vert \le \epsilon \\ \end{array}\right.$$

where $\epsilon$ is a value that is used as a threshold between L¹ and L² -norms.

IRLS can be easily incorporated in CG algorithms by including a weight $\bold W$ such that the operator $\bold L$ has a postmultiplier $\bold W$ and the the adjoint operator $\bold L^T$ has a premultiplier $\bold W^T$ Claerbout (2004). Even though we do not know the real L^p-norm residual vector at the beginning of the iteration, we can approximate the residual with a residual of the previous iteration step, and it will converge to a residual that is very close to the L^p-norm residual as the iteration step continues. This can be summarized as follows:

		 		 $\bold r \quad\longleftarrow\quad\bold L \bold m - \bold d$ 
		 iterate { 
		 		 $\bold W \quad\longleftarrow\quad{\bf diag}[f(\bold r)]$ 
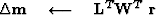
		 		  $\Delta\bold m \quad\longleftarrow\quad\bold L^T\bold W^T\ \bold r$ 
		 		  $\Delta\bold r\ \quad\longleftarrow\quad\bold W \bold L \ \Delta \bold m$ 
		 		  $(\bold m,\bold r) \quad\longleftarrow\quad{\rm cgstep}
 (\bold m,\bold r, \Delta\bold m,\Delta\bold r )$ 
		 		 }.