




Next: Iteratively Reweighted Least Squares
Up: Ji: Conjugate Guided Gradient
Previous: Ji: Conjugate Guided Gradient
Most inversion problems start by formulating the forward problem,
which describes the forward operator, 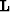 ,
that transforms the model vector
,
that transforms the model vector 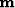 to the data vector
to the data vector 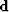 :
:
| 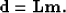 |
(1) |
In general, the measured data 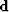 may be inexact, and
the forward operator
may be inexact, and
the forward operator 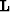 may be ill-conditioned.
In that case, instead of solving the above equation directly,
different approaches are used to find an optimum solution
may be ill-conditioned.
In that case, instead of solving the above equation directly,
different approaches are used to find an optimum solution 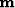 for a given data
for a given data 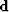 .The most popular method is finding a solution that minimizes the misfit between
the data
.The most popular method is finding a solution that minimizes the misfit between
the data 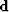 and the modeled data
and the modeled data 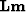 .The misfit, or the residual vector,
.The misfit, or the residual vector,  , is described as follows:
, is described as follows:
| 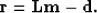 |
(2) |
In least-squares inversion, the solution 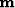 is the one that minimizes
the squares of the residual vector as follows:
is the one that minimizes
the squares of the residual vector as follows:
| 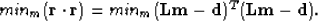 |
(3) |
Iterative solvers for the LS problem search the solution space
for a better solution in each iteration step,
along the gradient direction (in steepest-descent algorithms),
or on the plane made by the current gradient vector and
the previous descent-step vector (in conjugate-gradient algorithms).
Following Claerbout 1992,
a conjugate-gradient algorithm for the LS solution
can be summarized as follows:
 iterate {
iterate {
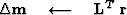
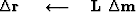
 } ,
} ,
where the subroutine cgstep() remembers
the previous iteration descent vector,
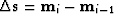 , where i is the iteration step,
and determines the step size by minimizing
the quadrature function composed from
, where i is the iteration step,
and determines the step size by minimizing
the quadrature function composed from
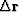 (the conjugate gradient)
and
(the conjugate gradient)
and 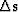 (the previous iteration descent vector),
as follows Claerbout (1992):
(the previous iteration descent vector),
as follows Claerbout (1992):
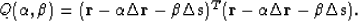
Notice that
the gradient vector (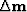 ) in the CG method for LS solution
is the gradient of the squared residual
and is determined by taking the derivative of the squared residual
(i.e. the L2-norm of the residual,
) in the CG method for LS solution
is the gradient of the squared residual
and is determined by taking the derivative of the squared residual
(i.e. the L2-norm of the residual, 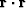 ,
with respect to the model
,
with respect to the model 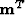 ):
):
| 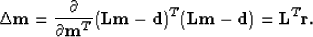 |
(4) |
iterate {
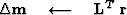
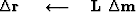
} ,
![]()