




Next: About this document ...
Up: Berryman: Seismic waves in
Previous: REFERENCES
Probably the most common way to write the linearized equations for the
phase velocities in VTI media (Thomsen, 1986; 2002; Rüger, 2002) is
| ![\begin{eqnarray}
V_p(\theta) \simeq V_{p0}\left[1 + \delta\sin^2\theta\cos^2\theta
+ \epsilon\sin^4\theta\right],
\end{eqnarray}](img162.gif) |
(64) |
| ![\begin{eqnarray}
V_{sv}(\theta) \simeq V_{s0}\left[1 +
{{V_{p0}^2}\over{V_{s0}^2}}(\epsilon-\delta)
\sin^2\theta\cos^2\theta\right],
\end{eqnarray}](img163.gif) |
(65) |
and
| ![\begin{eqnarray}
V_{sh}(\theta) \simeq V_{s0}\left[1 + \gamma\sin^2\theta\right].
\end{eqnarray}](img164.gif) |
(66) |
The approximations in all three cases are made based on assumed smallness of
the parameters 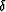 ,
,  ,
, 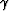 , which in fact may or may
not hold for any particular layered medium.
However, the work in this paper demands better approximations than
these, because the assumptions of weak anisotropy are always violated
in the cases of most interest, i.e., when the SV-wave velocity
actually does depend in a significant way on fluid content.
Thomsen (2002) (in his Appendix III) quotes another form of the
dispersion relation for
, which in fact may or may
not hold for any particular layered medium.
However, the work in this paper demands better approximations than
these, because the assumptions of weak anisotropy are always violated
in the cases of most interest, i.e., when the SV-wave velocity
actually does depend in a significant way on fluid content.
Thomsen (2002) (in his Appendix III) quotes another form of the
dispersion relation for 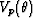 that is more useful for our
purposes (modified here to correct an obvious typo in the leading term):
that is more useful for our
purposes (modified here to correct an obvious typo in the leading term):
| 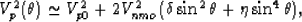 |
(67) |
where 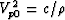 ,
, 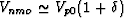 , and
, and
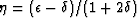 is the combination of
parameters introduced by Alkhalifah and Tsvankin (1996).
Although (67) is still an approximation, it is
much closer in form to the dispersion relation quoted here
in (34). The form (67) still assumes
smallness of the anisotropy parameters, but the usual square root
approximation has not been made yet, so the correspondence with
(34) is easier to scan. If we neglect higher order
contributions to
is the combination of
parameters introduced by Alkhalifah and Tsvankin (1996).
Although (67) is still an approximation, it is
much closer in form to the dispersion relation quoted here
in (34). The form (67) still assumes
smallness of the anisotropy parameters, but the usual square root
approximation has not been made yet, so the correspondence with
(34) is easier to scan. If we neglect higher order
contributions to 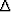 and thereby make the approximation that
and thereby make the approximation that
| 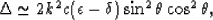 |
(68) |
then (34) becomes
| 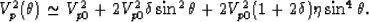 |
(69) |
If in addition we also make the small anisotropy approximations
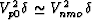 and
and 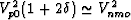 in (69),
then the result recovers (67).
in (69),
then the result recovers (67).
Our main goal in this Appendix is to make a direct comparison between
the exact formulas (34) and (35),
the approximate formulas resulting from (34) and
(35) when 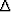 is replaced by its first
approximation (37), and either standard equations
(64) and (65) or approximation
(67)
and some yet to be determined companion equation for quasi-SV waves.
The easiest and most consistent way to arrive at an appropriate
approximate form for Vsv2 is to use the exact relations
(34) and (35) to determine what effective
value of
is replaced by its first
approximation (37), and either standard equations
(64) and (65) or approximation
(67)
and some yet to be determined companion equation for quasi-SV waves.
The easiest and most consistent way to arrive at an appropriate
approximate form for Vsv2 is to use the exact relations
(34) and (35) to determine what effective
value of 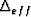 has been used in (67) and
then use it again in (35). We find
has been used in (67) and
then use it again in (35). We find
| 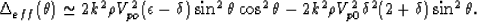 |
(70) |
However, this formula has the undesirable characteristic that it does
not vanish as it should for 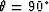 . The offending terms
are second order in
. The offending terms
are second order in 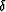 and therefore are usually neglected for
weak anisotropy. But the weak anisotropy assumptions implicit in
(67) are not valid in the present context, so
this is nevertheless a problem for us here. Making proper allowance for
this, we can arrive at a corrected
and therefore are usually neglected for
weak anisotropy. But the weak anisotropy assumptions implicit in
(67) are not valid in the present context, so
this is nevertheless a problem for us here. Making proper allowance for
this, we can arrive at a corrected 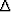 that has the desired behavior
and still agrees with the prior results under weak anisotropy conditions:
that has the desired behavior
and still agrees with the prior results under weak anisotropy conditions:
| 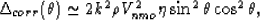 |
(71) |
and, therefore, that a good choice for Vsv2 to the same level of
approximation is
| 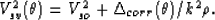 |
(72) |
But these modifications have led us back to the approximation
(34) and therefore provide nothing new. So instead of
comparisons to (67) and (72), we will
choose to make our comparisons to (64) and
(65). In particular, these two equations amount to using
| 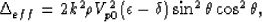 |
(73) |
except for some higher order corrections in 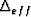 which would
always be small if the anisotropy were really always weak.
Although Eqs. (71) and (73) are
apparently the same, this fact is a bit misleading since
which would
always be small if the anisotropy were really always weak.
Although Eqs. (71) and (73) are
apparently the same, this fact is a bit misleading since 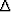 and
its corrections arise in the final results in different ways because
of differing square root approximations and different assumptions
about the presence or absence of strong anisotropy.
and
its corrections arise in the final results in different ways because
of differing square root approximations and different assumptions
about the presence or absence of strong anisotropy.
compvels
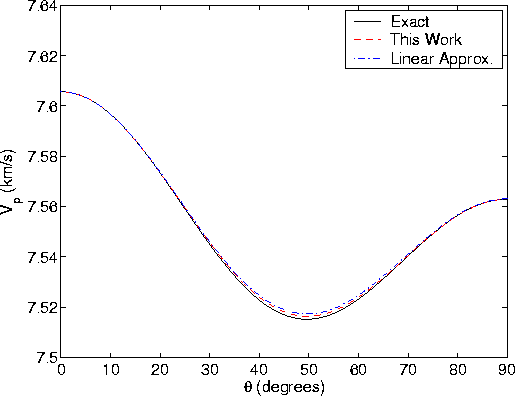
Figure 4 Compressional wave velocities
as computed exactly from the
dispersion relation (34), by (34) using approximation (37)
for 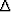 , and by the linear approximation (64).
This layered model is the same as in Figures 2 and 3 for the case B = 1.
, and by the linear approximation (64).
This layered model is the same as in Figures 2 and 3 for the case B = 1.

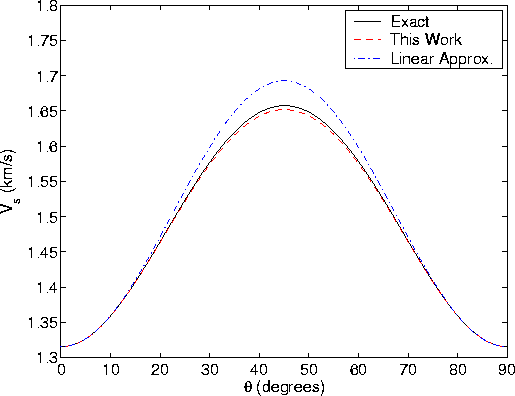
shearvels
Figure 5 Shear wave velocities
as computed exactly from the
dispersion relation (35), by (35) using approximation (37)
for 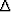 , and by the linear approximation (66).
This layered model is the same as in Figures 2 and 3 for the case B = 1.
, and by the linear approximation (66).
This layered model is the same as in Figures 2 and 3 for the case B = 1.

Numerical comparisons of these three sets of results for quasi-P and
quasi-SV waves are summarized in Figures 4 and 5 for one strong
anisotropy example. The comparison is obviously not a fair one for
the weak anisotropy equations since they are being used beyond their
acknowledged (and expected) range of validity. The main point of the
exercise is to see that the approximations made here give reasonable
approximations to the exact results for the full range of possible
incidence angles for strong anisotropy conditions, while the standard
results do not fair as well. All the methods agree quite well for
compressional waves in this model. The evaluation of (35)
using (37) to approximate 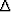 gives a clear improvement over
(65) for the quasi-SV wave velocity in a range of
intermediate angles. Overall, the weak anisotropy formulas
(64) and (65) give better results for
strong anisotropy in this case than might have been expected.
gives a clear improvement over
(65) for the quasi-SV wave velocity in a range of
intermediate angles. Overall, the weak anisotropy formulas
(64) and (65) give better results for
strong anisotropy in this case than might have been expected.





Next: About this document ...
Up: Berryman: Seismic waves in
Previous: REFERENCES
Stanford Exploration Project
5/23/2004
![]() is replaced by its first
approximation (37), and either standard equations
(64) and (65) or approximation
(67)
and some yet to be determined companion equation for quasi-SV waves.
The easiest and most consistent way to arrive at an appropriate
approximate form for Vsv2 is to use the exact relations
(34) and (35) to determine what effective
value of
is replaced by its first
approximation (37), and either standard equations
(64) and (65) or approximation
(67)
and some yet to be determined companion equation for quasi-SV waves.
The easiest and most consistent way to arrive at an appropriate
approximate form for Vsv2 is to use the exact relations
(34) and (35) to determine what effective
value of ![]() has been used in (67) and
then use it again in (35). We find
has been used in (67) and
then use it again in (35). We find
![]() gives a clear improvement over
(65) for the quasi-SV wave velocity in a range of
intermediate angles. Overall, the weak anisotropy formulas
(64) and (65) give better results for
strong anisotropy in this case than might have been expected.
gives a clear improvement over
(65) for the quasi-SV wave velocity in a range of
intermediate angles. Overall, the weak anisotropy formulas
(64) and (65) give better results for
strong anisotropy in this case than might have been expected.