




Next: Examples
Up: Lomask and Guitton: Adjustable
Previous: Introduction
In Lomask and Claerbout (2002), we found that we could integrate local dip information (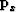 ) into total time shifts (
) into total time shifts (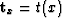 ) quickly in the Fourier domain with:
) quickly in the Fourier domain with:
| ![\begin{displaymath}
{\bf t}_x \quad \approx \quad {\rm FFT_{\rm 1D}}^{-1} \left[...
...\nabla'{\bf p}_x \right]}\ \over { -Z_x^{-1} +2 -Z_x} \right] ,\end{displaymath}](img3.gif) |
(1) |
where
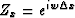 .
.
We also found that if we initialized the dips in the y direction (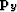 ) to zero, then this equation would apply some kind of regularization in the y direction:
) to zero, then this equation would apply some kind of regularization in the y direction:
| ![\begin{displaymath}
{\bf t} \quad \approx \quad {\rm FFT_{\rm 2D}}^{-1} \left[{\...
...} \right]}\ \over { -Z_x^{-1} -Z_y^{-1} +4 -Z_x -Z_y} \right] ,\end{displaymath}](img6.gif) |
(2) |
where
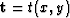 ,
, 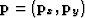 ,
, 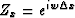 and
and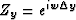 .This would cause the integration to be smooth in the y direction. However, we were not able to control how smooth it would be.
.This would cause the integration to be smooth in the y direction. However, we were not able to control how smooth it would be.
Here we will add an adjustable regularization parameter ( ) to equation (2). We begin with the fitting goal:
) to equation (2). We begin with the fitting goal:
| 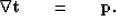 |
(3) |
We can minimize the difference between the estimated slope and the theoretical slope with:
| 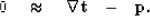 |
(4) |
Next, we write the quadratic form to be minimized as:
|  |
(5) |
Because the gradient is (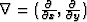 ), we can write:
), we can write:
| ![\begin{displaymath}
Q(\bold t) = \quad \left[ \begin{array}
{c} \frac{\bf \parti...
...{\bf \partial t}{\bf \partial y}-{\bf p}_y \end{array} \right].\end{displaymath}](img15.gif) |
(6) |
This can be rewritten as:
| 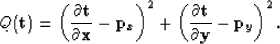 |
(7) |
The second term in equation (7) is the regularization term and only needs a scalar parameter  to adjust its weight relative to the first term. Now we have:
to adjust its weight relative to the first term. Now we have:
| 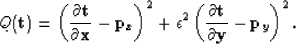 |
(8) |
Working backwards we see that it is now necessary to define a gradient operator that has an epsilon weight applied to one direction as:
| 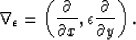 |
(9) |
It is also necessary to apply the scalar to the dip in the y direction as:
| 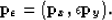 |
(10) |
Lastly, the y components of the z-transform in the denominator of equation (2) also need to be scaled. The final analytical solution with an adjustable regularization parameter is:
| ![\begin{displaymath}
{\bf t} \quad \approx \quad {\rm FFT_{\rm 2D}}^{-1} \left[{\...
...1} -\epsilon Z_y^{-1} +2+2\epsilon -Z_x -\epsilon Z_y} \right],\end{displaymath}](img20.gif) |
(11) |
where
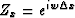 and
and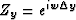 .
.





Next: Examples
Up: Lomask and Guitton: Adjustable
Previous: Introduction
Stanford Exploration Project
5/23/2004
![]() ) to zero, then this equation would apply some kind of regularization in the y direction:
) to zero, then this equation would apply some kind of regularization in the y direction:
![]() ) to equation (2). We begin with the fitting goal:
) to equation (2). We begin with the fitting goal:
![\begin{displaymath}
Q(\bold t) = \quad \left[ \begin{array}
{c} \frac{\bf \parti...
...{\bf \partial t}{\bf \partial y}-{\bf p}_y \end{array} \right].\end{displaymath}](img15.gif)