There are (at least) two possible ways to circumvent this issue. The first procedure involves using precomputed wavefields to train the phase-ray coordinate system by: i) establishing the longer wavelength rayfield structure by raytracing in a background velocity model using a broadband solver; ii) calculating an initial monochromatic wavefield solution using the background rayfield as the coordinate system; iii) computing an updated ray-coordinate system from the previous wavefield solution; and iv) calculating an updated wavefield on the improved phase-ray coordinate system. This procedure is addressed in companion paper Shragge and Biondi (2004) in this report.
A second approach is to use wavefields parameterized in phase-ray
coordinates, rather than Cartesian, to dictate the direction of the
next rayfront step.
For judiciously chosen ![]() steps, both the rayfield direction
and resulting wavefield evolves slowly, and ray directions differ by
only small, incremental amounts in a neighborhood of
steps, both the rayfield direction
and resulting wavefield evolves slowly, and ray directions differ by
only small, incremental amounts in a neighborhood of ![]() .
Hence, the orientation of previous few ray steps provide a good
estimate of the required ray direction at the present
.
Hence, the orientation of previous few ray steps provide a good
estimate of the required ray direction at the present ![]() step.
Thus, a phase-ray coordinate system may be computed on the fly using
the magnitude of the wavefield phase gradient of the previous
few steps and the local velocity function.
step.
Thus, a phase-ray coordinate system may be computed on the fly using
the magnitude of the wavefield phase gradient of the previous
few steps and the local velocity function.
Using a wavefield parameterized in ray-coordinates to generate the underlying coordinate system requires that the governing phase-ray equations are transformed accordingly. Fortunately, the magnitude of a scalar field gradient remains invariant to coordinate transformation, and is related through a change of variables,
| |
(11) |
| |
(12) |
![\begin{displaymath}
\left[\begin{array}[pos]
{c} \frac{\partial \phi}{\partial x...
...mma}\frac{\partial
\gamma}{\partial z} \\ \end{array}\right].\end{displaymath}](img44.gif) |
(13) |
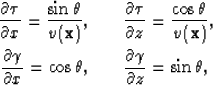 |
(14) | |
Computing a weighted average direction from the previous M steps
requires saving M+1 previous wavefield steps.
The discrete version of equation (12) for ray step at
index t, ![]() , is,
, is,
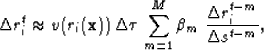 |
(15) |
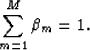 |
(16) |
The use of previous wavefield solutions to compute solutions to
equations (12) naturally gives rise to a broadened finite
difference stencil.
Figure 2 presents the finite difference stencil for
the M=2 case that has second-order accuracy in ![]() and
and ![]() .
.
|
stencil
Figure 2 Finite difference stencil for calculating wavefield solution at present step using the previous two steps (M=2). The solid square represents the location of the desired rayfield solution, and the in-filled circles connected by lines are the points contributing to the solution point. | 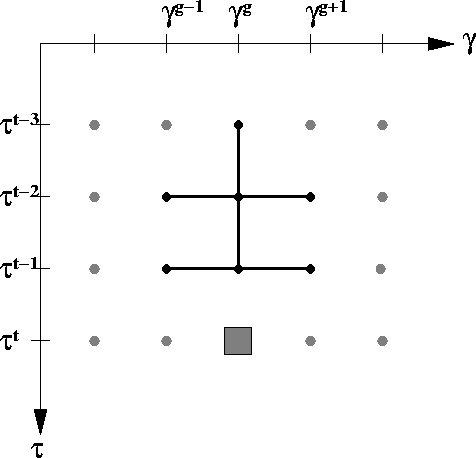 |