




Next: Ray-coordinate wavefield extrapolation
Up: Theory
Previous: Theory
A monochromatic acoustic wavefield, 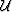 , at frequency,
, at frequency, 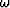 , and
spatial location,
, and
spatial location,  , may be represented by,
, may be represented by,
|  |
(1) |
where  and
and  are the amplitude and phase
functions, respectively.
For monochromatic waves propagating through isotropic media, the
gradient of phase function,
are the amplitude and phase
functions, respectively.
For monochromatic waves propagating through isotropic media, the
gradient of phase function,  , represents the
instantaneous direction of energy transport and is a characteristic to
the solution of the governing Helmholtz equation Foreman (1989).
Analogous to the ray precept in broadband theory, this
vector quantity defines the instantaneous direction and magnitude of
one ray in a continuous ray manifold. However, to differentiate
between the broadband and monochromatic ray representations, we
term the latter quantity phase-rays Shragge and Biondi (2003).
The governing differential equations for a phase-ray, ri, are
presented in the Exact-ray formulation of
Foreman (1989). In Cartesian coordinates, the subscript i on r
refers to the projection of the ray along the x and z axes - rx
and rz, respectively. The phase-ray equations, in summation
notation, are,
, represents the
instantaneous direction of energy transport and is a characteristic to
the solution of the governing Helmholtz equation Foreman (1989).
Analogous to the ray precept in broadband theory, this
vector quantity defines the instantaneous direction and magnitude of
one ray in a continuous ray manifold. However, to differentiate
between the broadband and monochromatic ray representations, we
term the latter quantity phase-rays Shragge and Biondi (2003).
The governing differential equations for a phase-ray, ri, are
presented in the Exact-ray formulation of
Foreman (1989). In Cartesian coordinates, the subscript i on r
refers to the projection of the ray along the x and z axes - rx
and rz, respectively. The phase-ray equations, in summation
notation, are,
| ![\begin{displaymath}
\frac{ {\rm d}r_i}{{\rm d}s} = \frac{ \partial\phi}{\partial...
...{ \partial
\phi}{\partial x_k}\right) \right]^ {-\frac{1}{2}},\end{displaymath}](img10.gif) |
(2) |
where  is the above phase function, xi is a coordinate of the
underlying Cartesian grid, and the repeated index k here (and
throughout the paper) represents a summation over all coordinate
indices. Scalar step magnitude,
is the above phase function, xi is a coordinate of the
underlying Cartesian grid, and the repeated index k here (and
throughout the paper) represents a summation over all coordinate
indices. Scalar step magnitude,  , is given by,
, is given by,
|  |
(3) |
where  is the velocity in the neighborhood of ray,
is the velocity in the neighborhood of ray,  ,and
,and  is an element of time along the ray.
is an element of time along the ray.
Calculating phase-rays thus requires isolating the gradient of the
monochromatic phase function.
An efficient procedure is to calculate the ratio of the wavefield
gradient to the wavefield itself,
|  |
(4) |
which eliminates the oscillatory nature of the wavefield. Taking the
imaginary component of equation (4),
|  |
(5) |
yields the required phase gradient.
The right hand side of equation (5) is calculable only when
a wavefield solution is known.
The solution for a ray, ri, is computed through integrating
the right hand sides of equations (2) using a
one-sided, non-stiff integration method (e.g. Simpson's 1/3 rule).
Interestingly, ray solutions are uniquely determined given an initial
starting position by reason that equations (2) form a
decoupled system of differential equations of first-order.
Accordingly, a phase-ray coordnate system is uniquely defined by
specifying of a set of initial coordinate points and a frequency,
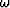 . Note that this specification makes the coordinate system
frequency dependent. Additional information on the theory of
phase-rays is discussed in both Shragge and Biondi (2003) and
Foreman (1989).
. Note that this specification makes the coordinate system
frequency dependent. Additional information on the theory of
phase-rays is discussed in both Shragge and Biondi (2003) and
Foreman (1989).





Next: Ray-coordinate wavefield extrapolation
Up: Theory
Previous: Theory
Stanford Exploration Project
5/23/2004