




Next: NW EXAMPLES
Up: Dynamic Programming
Previous: Needleman-Wunsch algorithm
There are two obvious problems with a straightforward
implementation of the NW algorithm.
Both are related to
the fact that our data is continuous, rather
then discrete.
We do not have the limited alphabet of the DNA example, so
our similarity matrix can't simply be matching
of values.
Therefore, a more appropriate measure of similarity in the seismic
case is a short-window correlation.
We capture this idea in a similarity function as
| 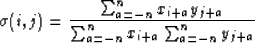 |
(6) |
or a semblance measure
| 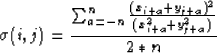 |
(7) |
where x and y are again the two traces, and n is the correlation
length.
The second problem is how to use our alignment data.
We are not dealing with discrete points but smooth functions. We
can estimate a prediction error filter Claerbout (1998)
or a time variant, non-stationary prediction error filter upon
the original data to describe the wavelet.
We have adopted this approach, allowing us to estimate
our aligned model 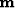 from our unaligned data
from our unaligned data 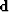 by
minimizing
by
minimizing
| 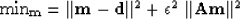 |
(8) |
where 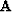 is filtering with the estimated prediction error filter and
is filtering with the estimated prediction error filter and
 is a scalar controlling how much weight to give the aligning.
This controls the relative importance of the alignment versus fitting the wavelet.
is a scalar controlling how much weight to give the aligning.
This controls the relative importance of the alignment versus fitting the wavelet.





Next: NW EXAMPLES
Up: Dynamic Programming
Previous: Needleman-Wunsch algorithm
Stanford Exploration Project
5/23/2004
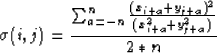
![]() from our unaligned data
from our unaligned data ![]() by
minimizing
by
minimizing