Squirt Flow Modeling Choices

To make numerical predictions of attenuation and dispersion, models must be proposed for the phase 2 (porous grain) parameters.

If the grains are modeled as spheres of radius R, the fluid-pressure gradient length within the grains can be estimated as $L_2=R/\sqrt{15}$ and the volume to surface ratio as V/S = R/(3v₂). The grain porosity is assumed to be in the form of microcracks and so it is natural to define an effective aperature h for these cracks. If the cracks have an average effective radius of R/N_R where N_R is roughly 2 or 3 and if there are on average N_c cracks per grain where N_c is also roughly 2 or 3 then the permeability and porsity of the grains is reasonably modeled as

$$\phi_2 = \frac{3 N_c}{4 N_R^2} \frac{h}{R} \mbox{\hskip6mm and \hskip4mm} k_2 = \phi_2 h^2/12$$ (127)

where $\phi_2$ is the fracture porosity within the porous grains. The dimensionless parameters k₂/L₂² and (v₂ V/S)/L₂ required in the expressions for $\gamma_{sq}$ and $\omega_{sq}$ are given by

$$\frac{k_2}{L_2^2} = \frac{15 N_c}{16 N_R^2} \left(\frac{h}{R... ...nd \hskip2mm} \left(\frac{v_2 V/S}{L_2}\right)^2 = \frac{5}{3}.$$ (128)

The normalized fracture aperature h/R is the key parameter in the squirt model.

The drained grain modulus K^d₂ is necessarily a function of the crack porosity $\phi_2$ (and therefore h/R). Real crack surfaces have micron (and smaller) scale asperities present upon them. If effective stress is applied in order to make the normalized aperature h/R smaller (so that, for example, the peak in squirt attenuation lies in the seismic band), new contacts are created that make the crack stronger. In the limit as $h/R \rightarrow 0$ (large effective stress), the cracks are no longer present and $K^d_2 \rightarrow K_s$where K_s is the mineral modulus of the grain.

Many models for such stiffening could be proposed. We intentionally make a conservative estimate here in proposing a simple linear porosity dependence $K^d_2 = K_s(1-\sigma \phi_2)$,where $\sigma$ is a fixed constant determined from fitting ultrasonic attenuation data. Effective medium theories [see, for example, Berryman et al. (2002)] predict that $\sigma$ should be inversely proportional to the aspect ratios of the cracks present. As a crack closes and asperities are brought into contact, there is naturally a decrease in $\phi_2$ but there should also be a decrease in $\sigma$ due to the fact that the remaining crack porosity becomes more spherical as new asperities come into contact. Taking $\sigma$ to be constant as crack porosity decreases is thus a minimalist estimate for how the drained modulus increases.

Thus, the porous-grain elastic properties are taken to be

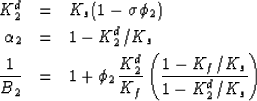$$\begin{eqnarray} K^d_2 &=& K_s {(1- \sigma \phi_2)} \\ \alpha_2 &=& 1 - K^d_2/K_... ...hi_2 \frac{K^d_2}{K_f} \left(\frac{1- K_f/K_s}{1-K^d_2/K_s}\right)\end{eqnarray}$$ (129) (130) (131)

where we have used the Gassmann fluid-substitution relations for $\alpha_2$ and B₂. The overall drained modulus K of the collection of porous (cracked) grains can be modeled for example as

$$K = \frac{K_2^d (1-v_1)}{1 + c v_1}$$ (132)

which is the same drained-modulus model as given in the appendix but with the solid grain modulus K_s replaced by the cracked grain modulus K₂^d.