Next: Toward broadband propagation
Up: Shragge and Biondi: Phase-rays
Previous: Phase-ray examples
This section examines the use of phase-rays as a coordinate
system for wavefield extrapolation.
The velocity model examined here (shown in figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) is characterized by a slow,
Gaussian-shaped velocity anomaly (-600 m/s) in a medium of otherwise
constant velocity (1200 m/s).
modelrays
a) is characterized by a slow,
Gaussian-shaped velocity anomaly (-600 m/s) in a medium of otherwise
constant velocity (1200 m/s).
modelrays
Figure 4 Gaussian-shaped velocity anomaly
model. a) Gaussian-shaped anomaly of -600 m/s maximum velocity
perturbation superposed on a constant 1200 m/s velocity field; b) 5
Hz wavefield computed for a shot located at 8000 m using a
single-velocity split step Fourier operator in Cartesian
coordinates; and c) phase-rays traced through the wavefield
of b).





This model was chosen to ensure that extrapolated wavefields
triplicate, as illustrated by figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
This wavefield was generated for a shot point located at 8000 m using
a split-step Fourier operator in a Cartesian coordinate system.
Figure
b.
This wavefield was generated for a shot point located at 8000 m using
a split-step Fourier operator in a Cartesian coordinate system.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows phase-rays traced through the
wavefield of figure
c shows phase-rays traced through the
wavefield of figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
Phase-rays in the upper portions of the model have fairly smooth coverage.
In areas of wavefield triplication, though, significant coverage gaps
are noticeable.
b.
Phase-rays in the upper portions of the model have fairly smooth coverage.
In areas of wavefield triplication, though, significant coverage gaps
are noticeable.
The phase-rays shown in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c were subsequently
used as a coordinate system for the generalized coordinate wavefield
extrapolation approach Sava and Fomel (2003). Figure
c were subsequently
used as a coordinate system for the generalized coordinate wavefield
extrapolation approach Sava and Fomel (2003). Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the velocity model of
figure
a shows the velocity model of
figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a in phase-ray coordinates.
a in phase-ray coordinates.
Reg.ER1.ssf.ps
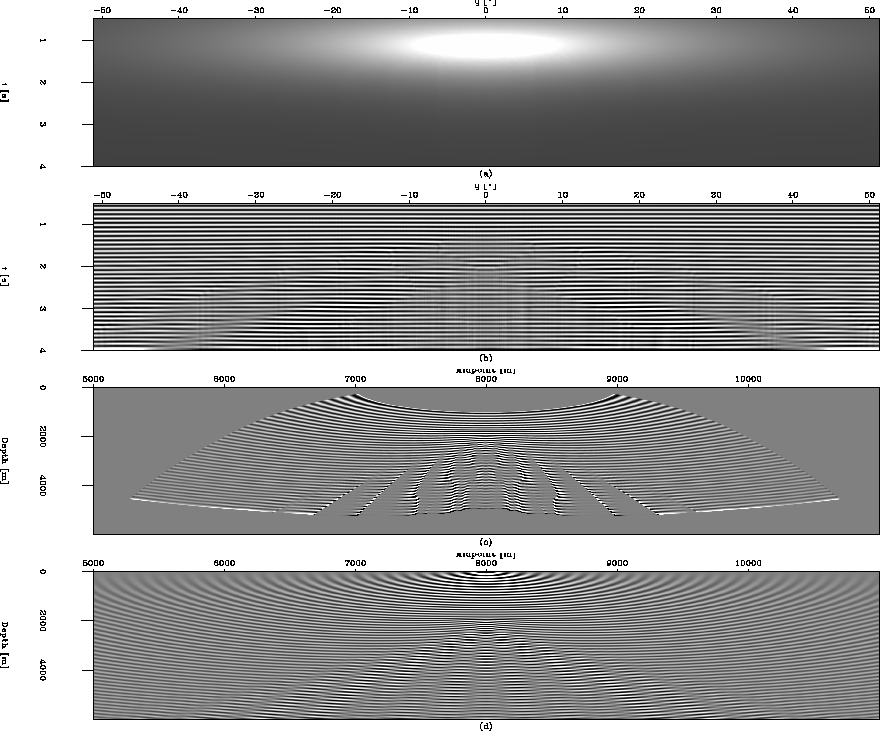
Figure 5 A comparison of wavefield
extrapolation results computed in phase-ray and Cartesian
coordinates. a) Velocity model of figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a
mapped to phase-ray coordinates; b) wavefield extrapolated in
phase-ray coordinates using a split-step Fourier method; c) the map
of wavefield in b) to Cartesian coordinates; d) wavefield solved in
Cartesian coordinates using a split-step Fourier operator.
a
mapped to phase-ray coordinates; b) wavefield extrapolated in
phase-ray coordinates using a split-step Fourier method; c) the map
of wavefield in b) to Cartesian coordinates; d) wavefield solved in
Cartesian coordinates using a split-step Fourier operator.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b presents the results of wavefield
extrapolation in phase-ray coordinates using a split-step Fourier
operator and the velocity model shown in figure
b presents the results of wavefield
extrapolation in phase-ray coordinates using a split-step Fourier
operator and the velocity model shown in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a.
Figure
a.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows this result mapped to Cartesian
coordinates.
The wavefield presented in figure
c shows this result mapped to Cartesian
coordinates.
The wavefield presented in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d was
computed in Cartesian coordinates using a split-step Fourier
operator.
In areas where wavefields are present in significant amplitude, the
phase-ray and Cartesian results are similar.
Areas of low wavefield amplitude beneath the Gaussian velocity
anomaly (e.g. [z,x]=[4200 m,6800 m]), though, are markedly different.
This difference is related to the inability to map the results from ray
coordinates to Cartesian in areas of minimal or non-existent ray coverage.
d was
computed in Cartesian coordinates using a split-step Fourier
operator.
In areas where wavefields are present in significant amplitude, the
phase-ray and Cartesian results are similar.
Areas of low wavefield amplitude beneath the Gaussian velocity
anomaly (e.g. [z,x]=[4200 m,6800 m]), though, are markedly different.
This difference is related to the inability to map the results from ray
coordinates to Cartesian in areas of minimal or non-existent ray coverage.
This experiment highlights a consequence of using phase-ray
coordinates for wavefield extrapolation.
Monochromatic wavefield triplication is generally identified by
interference patterns created by converging wavefield components.
(See, for example, the checkerboard pattern beneath the Gaussian velocity anomaly.)
Because phase-ray direction is dependent on the total wavefield gradient,
it is similarly dependent on the gradients of each
converging wavefield component.
The gradient vector, being unable to unwrap individual convergent phases,
chooses a weighted average of individual gradients.
Accordingly, phase-rays are usually steered in the direction of the
convergent component with the largest individual gradient magnitude,
but they will never triplicate since the weighted gradient is uniquely
defined at each wavefield point.
This fact suggests that phase-ray coordinates represent a
trade off between introducing inaccuracy associated with triplicating
coordinates and inaccuracy of wavefield extrapolation at greater angles
to the phase-ray direction.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a comparison between
wavefields extrapolated in phase-ray and conventional ray coordinates
Sava and Fomel (2003).
presents a comparison between
wavefields extrapolated in phase-ray and conventional ray coordinates
Sava and Fomel (2003).
Jeff.ER1.ssf.ps
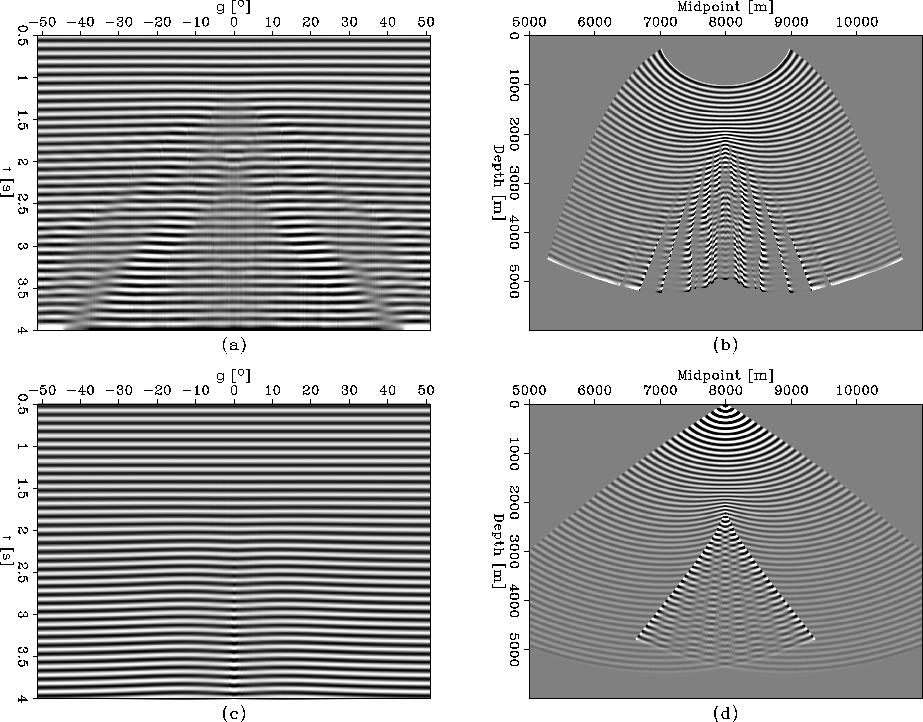
Figure 6 A comparison of wavefield
extrapolation results computed in phase-ray and conventional ray
coordinates. a) wavefield extrapolated in phase-ray coordinates; b)
wavefield of a) interpolated into Cartesian coordinates; c)
wavefield extrapolated in conventional ray coordinates
Sava and Fomel (2003); and d) wavefield of c) interpolated in
Cartesian coordinates.





Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and
a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
present wavefields extrapolated in phase-ray coordinates and after
interpolation into Cartesian coordinates, respectively.
Figures
b
present wavefields extrapolated in phase-ray coordinates and after
interpolation into Cartesian coordinates, respectively.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c and
c and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d
present similar results, but with conventionally traced rays.
Of the two ray coordinate systems tested, the phase-ray coordinate
extrapolated wavefield (figure
d
present similar results, but with conventionally traced rays.
Of the two ray coordinate systems tested, the phase-ray coordinate
extrapolated wavefield (figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b)
better resembles the wavefield calculated in Cartesian coordinates (figure
b)
better resembles the wavefield calculated in Cartesian coordinates (figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c).
However, the sampling of phase-ray extrapolated wavefields, and their
Cartesian maps, must be greatly improved before a definitive
comparison is possible.
c).
However, the sampling of phase-ray extrapolated wavefields, and their
Cartesian maps, must be greatly improved before a definitive
comparison is possible.
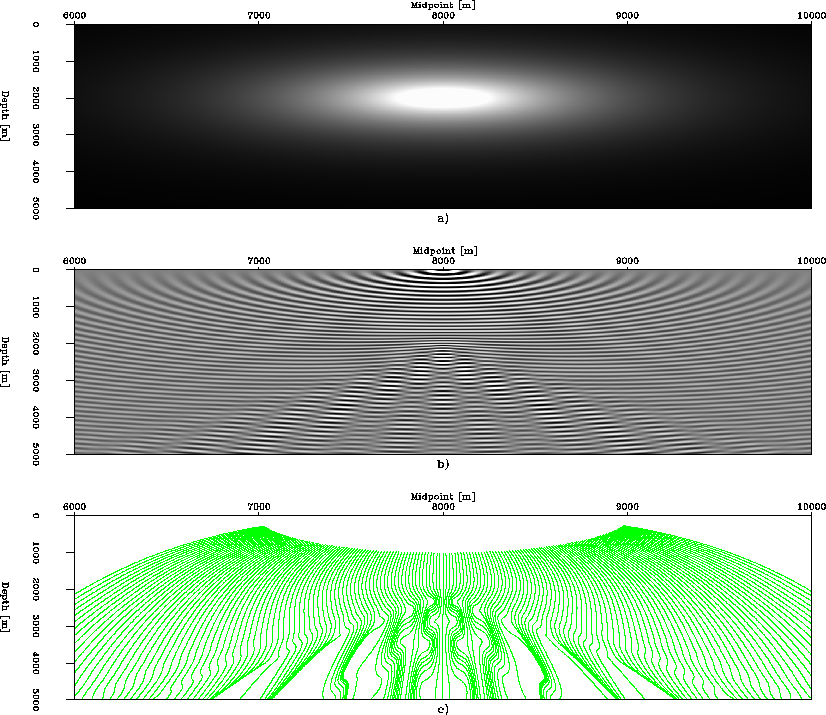
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) is characterized by a slow,
Gaussian-shaped velocity anomaly (-600 m/s) in a medium of otherwise
constant velocity (1200 m/s).
a) is characterized by a slow,
Gaussian-shaped velocity anomaly (-600 m/s) in a medium of otherwise
constant velocity (1200 m/s).