Next: Residual moveout in the
Up: Shan and Biondi: Residual
Previous: Introduction
Most current migration velocity analysis methods
Clapp (2001); Sava and Biondi (2003)
are based on the curvature information from Angle-Domain CIGs(ADCIGs),
which are created from the migration cube Sava and Fomel (2003).
When the migration velocity is the
true velocity, the ADCIG at a reflection point is a flat line. When the migration velocity
is inaccurate, the curvature parameters estimated from ADCIGs can be back-projected
and inverted for velocity updates. Biondi and Symes (2003) demonstrates that in an ADCIG cube,
the image point lies on the line normal to the apparent reflector dip, passing through the
point where the source ray intersects the receiver ray.
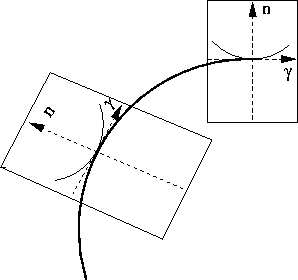
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIGs at reflection points of different dip angles.
Under the stationary-raypath assumption, the shift of the image point along the normal direction is
Biondi and Symes (2003)
shows the ADCIGs at reflection points of different dip angles.
Under the stationary-raypath assumption, the shift of the image point along the normal direction is
Biondi and Symes (2003)
| 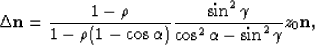 |
(1) |
where 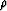 is the constant scaling factor of the slowness,
is the constant scaling factor of the slowness,  is dip angle of the reflector,
is dip angle of the reflector,
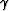 is the opening angle,
is the opening angle, 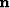 is the normal direction vector of the reflection point,
and z0 is the depth at the reflection point.
For flat reflectors, the shift (1) reduces to
is the normal direction vector of the reflection point,
and z0 is the depth at the reflection point.
For flat reflectors, the shift (1) reduces to
| 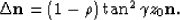 |
(2) |
Equations (1) and (2) can be used to estimate the curvature parameters for velocity
analysis. However, to estimate
the curvature parameters caused by local velocity perturbation, we don't consider the effect of depth z0.
ball
Figure 1 ADCIGs with different dip angles. 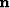 is the normal
direction vector, and
is the normal
direction vector, and 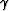 is the opening angle.
is the opening angle.






Next: Residual moveout in the
Up: Shan and Biondi: Residual
Previous: Introduction
Stanford Exploration Project
10/14/2003
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIGs at reflection points of different dip angles.
Under the stationary-raypath assumption, the shift of the image point along the normal direction is
Biondi and Symes (2003)
shows the ADCIGs at reflection points of different dip angles.
Under the stationary-raypath assumption, the shift of the image point along the normal direction is
Biondi and Symes (2003)