




Next: Irregular Traces
Up: Curry: Prediction-error filter estimation
Previous: Introduction
A prediction-error filter is estimated by solving a minimization problem where known data is convolved (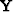 ) with
an unknown filter (
) with
an unknown filter ( ), so
), so
| 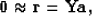 |
(1) |
where the first coefficient of  is constrained to be unity. This can be written as
is constrained to be unity. This can be written as
| 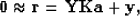 |
(2) |
where 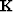 is a mask for the first PEF coefficient, and
is a mask for the first PEF coefficient, and 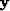 is simply a copy of the data.
Writing out the matrices for a PEF with 3 coefficients and for 7 data samples looks like
is simply a copy of the data.
Writing out the matrices for a PEF with 3 coefficients and for 7 data samples looks like
| ![\begin{displaymath}
\bold 0
\quad \approx \quad
\bold r =
\left[
\begin{array}
...
... \\
y_3 \\
y_4 \\
y_5 \\
y_6 \end{array} \right]
.\end{displaymath}](img7.gif) |
(3) |
The previous equations have all been for a 1D case. By use of the helical coordinate
Claerbout (1998), these equations can easily be extended to higher dimensions.
In the case of missing data, a diagonal weight (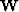 ) can be introduced that is when
a missing data point is in the equation, and 1 where all data are present. This weight can
also be used to eliminate edge effects caused by helical convolution.
) can be introduced that is when
a missing data point is in the equation, and 1 where all data are present. This weight can
also be used to eliminate edge effects caused by helical convolution.
When data are interlaced, a PEF can be estimated by spacing filter coefficients during convolution,
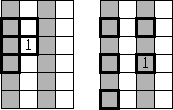
so that they fall on known data. An example of this filter spacing is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The problem with this methods is that the data must be regularly sampled in all dimensions.
.
The problem with this methods is that the data must be regularly sampled in all dimensions.
interlace
Figure 1 Examples of PEFs on interlaced data. White bins are empty, gray have data. Left: A PEF
cannot be estimated due to too much missing data. Right: The spaced PEF can be estimated on interlaced data.
|
|  |






Next: Irregular Traces
Up: Curry: Prediction-error filter estimation
Previous: Introduction
Stanford Exploration Project
10/14/2003
![\begin{displaymath}
\bold 0
\quad \approx \quad
\bold r =
\left[
\begin{array}
...
... \\
y_3 \\
y_4 \\
y_5 \\
y_6 \end{array} \right]
.\end{displaymath}](img7.gif)
![]() ) can be introduced that is when
a missing data point is in the equation, and 1 where all data are present. This weight can
also be used to eliminate edge effects caused by helical convolution.
) can be introduced that is when
a missing data point is in the equation, and 1 where all data are present. This weight can
also be used to eliminate edge effects caused by helical convolution.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The problem with this methods is that the data must be regularly sampled in all dimensions.
.
The problem with this methods is that the data must be regularly sampled in all dimensions.
