Relation of TLS to Damped Least-squares (DLS)

The TLS solution is closely related to the classic damped least squares (DLS) solution, where the damping factor, $\sigma^2$, is the smallest nonzero singular value of the augmented matrix $[\bf L \;\; d ]$: 

$$\bold m_{DLS} = \left(\bold L^T \bold L + \sigma^2 \bold I \right)^{-1} \bold L^T \bf d.$$ (128)

The TLS solution can be rewritten (, ) as follows.  

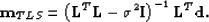$$\bold m_{TLS} = \left(\bold L^T \bold L - \sigma^2 \bold I \right)^{-1} \bold L^T \bf d.$$ (129)

The only difference between equations () and () is the negative sign on the damping term. Thus the TLS problem is considered a ``deregularization'' of the standard LS problem, and is guaranteed to be worse conditioned, since $\bold L^T \bold L$ is positive-semidefinite at worst ().