Rosales et al. (2001) describe three
possible ways to perform residual migration.
The most precise method is an exact derivation
which involves the combination of the ![]() ,
, ![]() and
and ![]() parameters.
This method attempts to simultaneously correct the effect of
two inaccurate velocity fields.
parameters.
This method attempts to simultaneously correct the effect of
two inaccurate velocity fields.
Assuming that the initial migration was done with the velocities v0p and v0s, and that the correct velocities are vmp and vms, we can then write
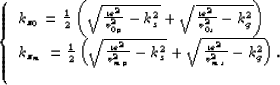 |
Solving for ![]() in the
first equation of (1) and substituting it
in the second equation of (1), we obtain
the expression for prestack Stolt depth residual migration
for converted waves:
in the
first equation of (1) and substituting it
in the second equation of (1), we obtain
the expression for prestack Stolt depth residual migration
for converted waves:
| |
(1) |
where ![]() is the transformation kernel defined as:
is the transformation kernel defined as:
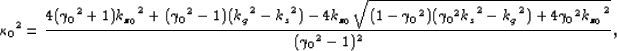
and ![]() ,
, ![]() , and
, and ![]() .
.
This formulation depends only on velocity ratios. This fact implies that it is a valid formulation for non-constant velocity media, as suggested by Sava (2000).