




Next: Test with synthetic data
Up: Valenciano and Biondi: Deconvolution
Previous: Deconvolution in the Fourier
In equation (9) the reflectivity strength is affected by the bandwidth of the data.
Let us consider the case where the source and receiver wavefields coincide at the reflector depth and both have a similar frequency content. The best situation we could have is for their division to be a box function. This is unlikely to happen in a real case. Inside the data bandwidth the division is a constant value. But outside of the data bandwidth we may try to divide small numbers by small numbers, which has the potential to be unstable. In equation (8) we use a damping factor to avoid this source of instability but when we apply equation (9) we end up with values that were supposed to be zero contributing to the reflectivity strength.
A different implementation of equation (8), forcing hard zeros when 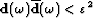 , reduces the impact of band-limited data in the reflectivity strength calculation as
, reduces the impact of band-limited data in the reflectivity strength calculation as
| 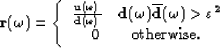 |
(8) |
There is another source of error for the band-limited.
The Fourier pair of the box function is a sinc function. In the extreme case of a infinite wide box the Fourier pair is a delta function centered at zero lag. As the box is getting narrower in the Fourier domain, the delta becomes a wider sinc function in the time domain. Therefore, the reflectivity strength 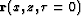 is a scaled version of his infinite bandwidth version.
We can compensate for the bandwidth of the data by computing the zero lag of the deconvolution as
is a scaled version of his infinite bandwidth version.
We can compensate for the bandwidth of the data by computing the zero lag of the deconvolution as
| 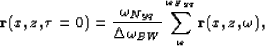 |
(9) |
where 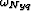 is the Nyquist frequency and
is the Nyquist frequency and 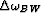 is the bandwidth, then zero lag of the deconvolution corresponds to the reflectivity strength. In this case the bandwidth
is the bandwidth, then zero lag of the deconvolution corresponds to the reflectivity strength. In this case the bandwidth 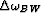 is defined as the frequency range where the inequality
is defined as the frequency range where the inequality 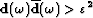 holds.
holds.





Next: Test with synthetic data
Up: Valenciano and Biondi: Deconvolution
Previous: Deconvolution in the Fourier
Stanford Exploration Project
11/11/2002
![]() , reduces the impact of band-limited data in the reflectivity strength calculation as
, reduces the impact of band-limited data in the reflectivity strength calculation as
![]() is a scaled version of his infinite bandwidth version.
We can compensate for the bandwidth of the data by computing the zero lag of the deconvolution as
is a scaled version of his infinite bandwidth version.
We can compensate for the bandwidth of the data by computing the zero lag of the deconvolution as