Implementation of a 2D, zero-offset, constant-velocity $\omega$-x SMM

Although it is not easy to find irregularly sampled zero-offset non-synthetic reflection datasets, such a case was chosen for investigation because of its simplicity; any results should be directly applicable to the prestack case.

The Appendix shows a derivation for the $15^\circ$ (parabolic) wave equation (38) and for the $45^\circ$ one (37). Both can be expressed as:

 

a Q_xxz + Q_xx + b Q_z = 0,

where the subscripts denote partial derivatives along the corresponding axes. Plugging in the templates in (8), (9) (10), we get:

 

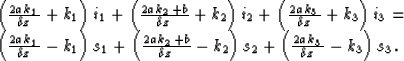$$\begin{array} {l} \left( {\frac{{2{\kern 1pt} a{\kern 1pt} ... ...n 1pt} k_3 }}{{\delta z}} - k_3 } \right)s_3. \\ \end{array}$$ (12)

In the case of the $15^\circ$ equation, a=0, and for the $45^\circ$one, $a = \frac{iv}{2\omega}$. In both cases $b = \frac{2i\omega}{v}$. They are the same as for the regular sampling case, which is simply a particular case of this equation (with particular values of k_i). The stability of the downward continuation undertaken in this manner is proven for all practical purposes by the results in Figs. 3 and 4. This means that the special stability precautions taken by Dellinger and Muir (1986) are an unnecessary complication.

The resulting tridiagonal system is solved and the values of $Q(\omega, x, z_2)$ are found. The lens term (40) which is applied after each downward continuation step with the above described equations does not depend in any way on the sampling of the x-axis and is therefore the same as in $\omega$ - x migrations of evenly sampled data.

Unfortunately, the so-called 1/6 trick [Claerbout (1985b), section 4.3] cannot be straightforwardly applied when the spatial axis is unevenly sampled. With a bit of work, an equivalent formula can also be deduced for the irregular sampling case.

The proof in the Appendix ensures that no hidden regular sampling assumption has been incorporated in the $15^\circ$ and $45^\circ$ wave equation approximations.