To allow the possible solutions to change radically (sometimes necessary
to escape local minima), I tried an algorithm that tries random but
smooth solutions at the beginning when the temperature is hot.
As the temperature cools, it tries solutions that have more and more
roughness.
Rather than randomly changing all of the components of ![]() ,only a few widely spaced samples are randomly changed.
Then the rest of the points are interpolated between them and the
energy is calculated over the interpolated line.
,only a few widely spaced samples are randomly changed.
Then the rest of the points are interpolated between them and the
energy is calculated over the interpolated line.
| |
(4) |
This process is repeated and the sampling interval becomes smaller and smaller with increasing interations. This method does not require the use of the probability to get convergence, although that may still have its use later.
A computation template for this method is
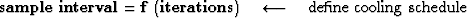
iterate {

if
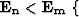
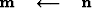
}
At coarse sampling intervals, the function is inherently smooth but as the sampling interval gets smaller and smaller, the trial solutions may become too rough. Therefore, I added an additional constraint on the maximum amount of roughness allowed. This results in throwing out trial solutions only near the end when the sampling interval is very small.
 |
 |
Figure 10 shows a frame taken early on in the estimation process. The large dots show the randomly moving points and the dashed line is the interpolated line. Figure 11 shows another frame taken later; the density of the dots illustrates the shrinking sampling interval.