![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
Accurate velocity estimation is essential to obtain a good migrated image and accurate resevoir attributes Claerbout (1999). The problem is that tomographic velocity estimation is an underdetermined problem. We can reduce the null space of the tomographic process by adding additional constraints, or more accurate goals, to the estimation. In early work Clapp et al. (1997); Clapp and Biondi (1999); Clapp (2001a,b) I discussed one such constraint: encouraging velocity follows dip. Often we have an added constraint; although we may be unsure of reflector position (due to anisotropy, etc.) or we may have a good estimate of reflector dip (either from well logs, geologic models, etc). By incorporating this information into the inversion we can better constrain the inversion process. This method is tested on a fairly complicated synthetic dataset.
THEORY
Tomography is a non-linear problem that we linearize
around an initial slowness model. In this discussion I will
be talking about the specific case of ray based tomography but
most of the discussion is valid for other tomographic operators.
We can linearize the problem around an initial slowness model and
obtain a linear relation ![]() between
the change in travel times
between
the change in travel times ![]() and
change in slowness
and
change in slowness ![]() and reflector position
and reflector position ![]() . We
break up our tomography operator into its two parts, changes
due to slowness along the ray
. We
break up our tomography operator into its two parts, changes
due to slowness along the ray ![]() and changes due to reflector movement
and changes due to reflector movement
![]() :
:
| (1) |
| (2) |
| (3) |
We can approximate the change in reflector position due to a change in slowness by assuming movement normal to the reflector and integrating along the normal ray,
| (4) |
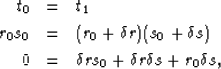 |
(5) | |
| (6) |
For simplicity let's concern ourselves with the 2-D problem, though
it's easily extendible to 3-D.
Imagine that ![]() represents our a priori reflector dip,
represents our a priori reflector dip, ![]() is a
derivative operator,
is a
derivative operator, ![]() is our final reflector dip,
is our final reflector dip,
![]() is the initial reflector position,
and
is the initial reflector position,
and ![]() is our change in reflector position. We can derive
a fairly simple fitting goal relating reflector dip
and
is our change in reflector position. We can derive
a fairly simple fitting goal relating reflector dip
and ![]() ,
,
 |
||
| (7) | ||
If we combine this new fitting goal with our tomographic fitting goal and our regularization fitting goal we get,
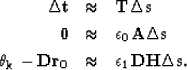 |
||
| (8) | ||
EXAMPLE To test the methodology I decided to use a synthetic 2-D dataset generated by BP based on a typical North Sea environment, Figure 1. To avoid tomography's problem with sharp velocity contrasts I chose to assume an accurate knowledge of the velocity structure down to 1.8 km. For the remaining initial velocity structure I smoothed the correct velocity. Figure 2 shows the initial velocity model and initial migration.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
I then performed two different series of tomography loops.
In the first case I used a standard approach, without the
constraint on dip of the basement reflector at 4 km.
Figure 3 shows the initial migration with
my pick of the reflector position overlaid (![]() in
fitting goals (8)). Figures 4
and 5 show the velocity and migration
result after a single non-linear iteration of tomography using
both approaches.
In the first iteration
the velocity structure looks somewhat more accurate without
the dip constraint.
The image tells a different story. Note
how the bottom reflector is much flatter using the dip constraint
condition (Figure 5) and the overall image
positioning is a little better. After four iterations, we see a more
dramatic difference. Without the dip constraint condition (Figure 6)
the velocity model is having trouble converging, especially along
the right edge. The bottom reflector is quite discontinuous and
misplaced. The overall image quality is disappointing. With the dip
constraining condition (Figure 7)
the velocity model is correctly finding the salt boundaries. The
bottom reflector is fairly flat, consistent, and well positioned.
The overall image quality is better than the result without
the dip constraint.
in
fitting goals (8)). Figures 4
and 5 show the velocity and migration
result after a single non-linear iteration of tomography using
both approaches.
In the first iteration
the velocity structure looks somewhat more accurate without
the dip constraint.
The image tells a different story. Note
how the bottom reflector is much flatter using the dip constraint
condition (Figure 5) and the overall image
positioning is a little better. After four iterations, we see a more
dramatic difference. Without the dip constraint condition (Figure 6)
the velocity model is having trouble converging, especially along
the right edge. The bottom reflector is quite discontinuous and
misplaced. The overall image quality is disappointing. With the dip
constraining condition (Figure 7)
the velocity model is correctly finding the salt boundaries. The
bottom reflector is fairly flat, consistent, and well positioned.
The overall image quality is better than the result without
the dip constraint.
|
picked
Figure 3 The initial migrated model overlaid by the picked initial reflector position. |  |
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)