Next: Shaping filters and the
Up: A simple 1D problem
Previous: A simple 1D problem
h
This section illustrates some limitations of the  -norm
for the estimation of shaping filters.
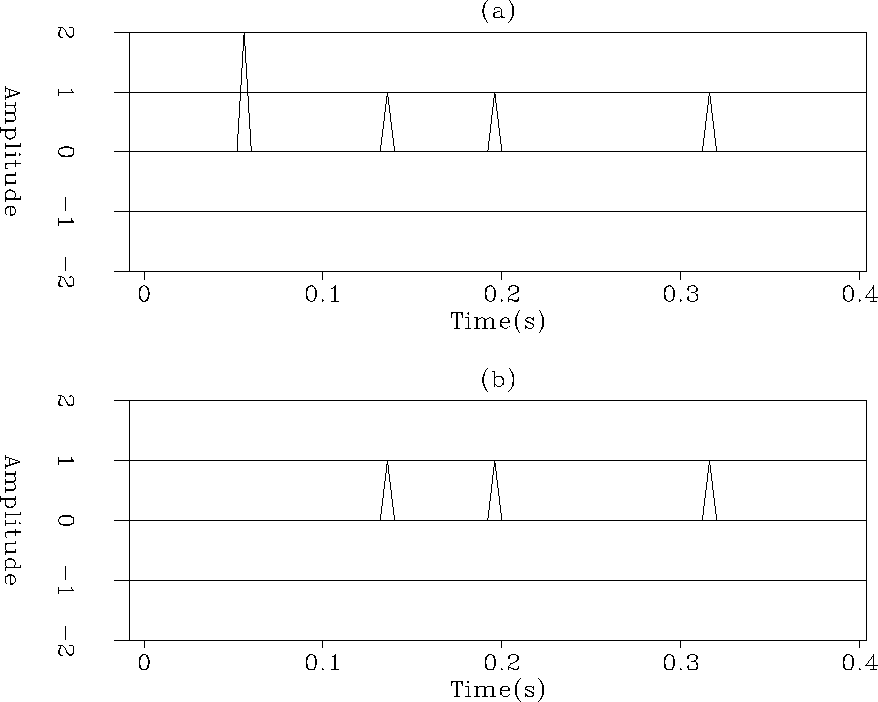
In figure 1, we display a very simple 1D problem.
On the top we have four events corresponding to one primary
(on the left) and three multiples (on the right). Note that the primary has
higher amplitude than the multiples. On the bottom we
show a multiple model that exactly corresponds to the real multiples.
Our goal is to estimate one shaping filter
-norm
for the estimation of shaping filters.
In figure 1, we display a very simple 1D problem.
On the top we have four events corresponding to one primary
(on the left) and three multiples (on the right). Note that the primary has
higher amplitude than the multiples. On the bottom we
show a multiple model that exactly corresponds to the real multiples.
Our goal is to estimate one shaping filter 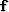 that minimizes
the objective function
that minimizes
the objective function
| 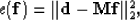 |
(1) |
where 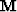 is the matrix representing the convolution with
the time series for the multiple model (Figure
1b) and
is the matrix representing the convolution with
the time series for the multiple model (Figure
1b) and 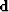 the time
series for the data (Figure 1a).
the time
series for the data (Figure 1a).
Now, if we estimate the filter 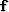 with enough degrees of freedom
(enough coefficients) to minimize equation (1),
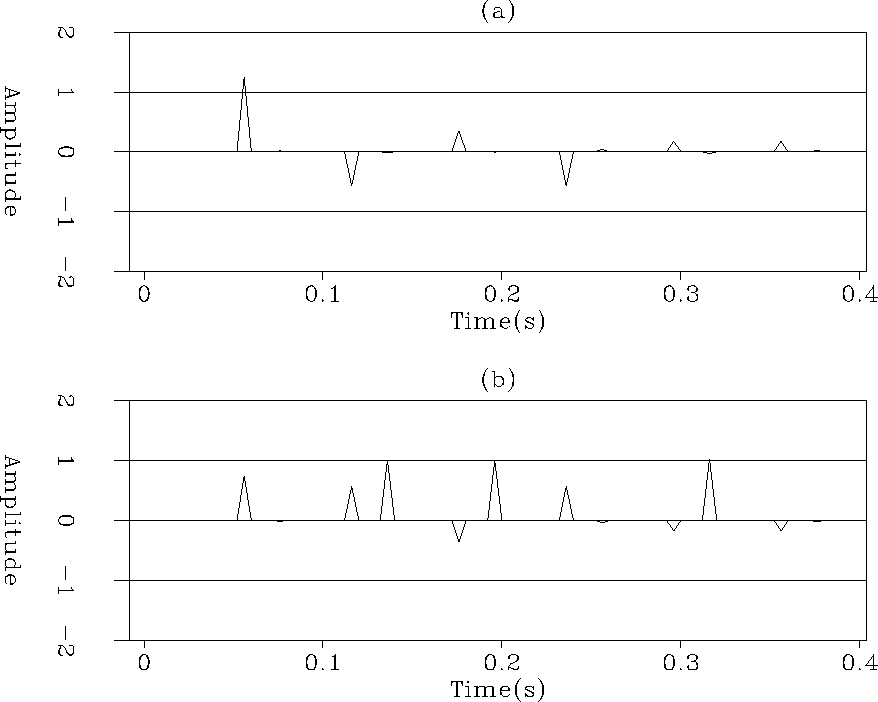
we obtain for the signal Figure 2a, and for
the noise Figure 2b.
The estimated signal does not resemble the primary in Figure 1a.
We show the corresponding shaping filter in Figure 3.
This filter is not the single spike at lag=0 that we desire. The problem stems from
the least-squares criterion which yields an estimated signal that has, by definition,
minimum energy. In this 1D case, the total energy in the estimated
signal (Figure 2a) is e=2.4, which is less than the
total energy of the primary alone
(e=4). This is the fundamental problem if we use the
with enough degrees of freedom
(enough coefficients) to minimize equation (1),
we obtain for the signal Figure 2a, and for
the noise Figure 2b.
The estimated signal does not resemble the primary in Figure 1a.
We show the corresponding shaping filter in Figure 3.
This filter is not the single spike at lag=0 that we desire. The problem stems from
the least-squares criterion which yields an estimated signal that has, by definition,
minimum energy. In this 1D case, the total energy in the estimated
signal (Figure 2a) is e=2.4, which is less than the
total energy of the primary alone
(e=4). This is the fundamental problem if we use the 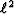 -norm to
estimate the shaping filter. In the next section, we show that the
-norm to
estimate the shaping filter. In the next section, we show that the 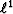 norm should be used if amplitude differences exist between primaries
and multiples.
norm should be used if amplitude differences exist between primaries
and multiples.
datmul
Figure 1 (a) The data with one
primary on the left, and three multiples on the right. (b) The
multiple model that we want to adaptively subtract from (a).




 1Dl2
1Dl2
Figure 2 (a) The signal estimated with the
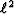 -norm. (b) The noise estimated with the
-norm. (b) The noise estimated with the 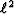 -norm.
-norm.





filterl2
Figure 3 Shaping filter estimated for the
1D problem with the 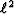 -norm. This filter is not a single
spike at lag=0. -norm. This filter is not a single
spike at lag=0.
|
|  |










Next: Shaping filters and the
Up: A simple 1D problem
Previous: A simple 1D problem
Stanford Exploration Project
6/7/2002
![]() with enough degrees of freedom
(enough coefficients) to minimize equation (1),
we obtain for the signal Figure 2a, and for
the noise Figure 2b.
The estimated signal does not resemble the primary in Figure 1a.
We show the corresponding shaping filter in Figure 3.
This filter is not the single spike at lag=0 that we desire. The problem stems from
the least-squares criterion which yields an estimated signal that has, by definition,
minimum energy. In this 1D case, the total energy in the estimated
signal (Figure 2a) is e=2.4, which is less than the
total energy of the primary alone
(e=4). This is the fundamental problem if we use the
with enough degrees of freedom
(enough coefficients) to minimize equation (1),
we obtain for the signal Figure 2a, and for
the noise Figure 2b.
The estimated signal does not resemble the primary in Figure 1a.
We show the corresponding shaping filter in Figure 3.
This filter is not the single spike at lag=0 that we desire. The problem stems from
the least-squares criterion which yields an estimated signal that has, by definition,
minimum energy. In this 1D case, the total energy in the estimated
signal (Figure 2a) is e=2.4, which is less than the
total energy of the primary alone
(e=4). This is the fundamental problem if we use the ![]() -norm to
estimate the shaping filter. In the next section, we show that the
-norm to
estimate the shaping filter. In the next section, we show that the ![]() norm should be used if amplitude differences exist between primaries
and multiples.
norm should be used if amplitude differences exist between primaries
and multiples.