




Next: Results
Up: Karpushin and Brown: PEFs
Previous: Data Description
The problem of interpolating irregularly sampled data, like the Galilee data
set, onto a regular grid to produce a map can
be written in terms of the fitting goals of an inverse linear
interpolation problem Claerbout (1999):
| 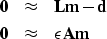 |
|
| (1) |
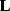 is the linear operator which maps data onto
the map. Usually
is the linear operator which maps data onto
the map. Usually 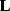 is either a binning or a bilinear interpolation
operator. The second equation in system (1) is a
regularization term where
is either a binning or a bilinear interpolation
operator. The second equation in system (1) is a
regularization term where 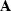 is a roughening operator that
imposes smoothness of the model in this underdetermined
problem, at the price of fitting data exactly.
Everywhere below,
is a roughening operator that
imposes smoothness of the model in this underdetermined
problem, at the price of fitting data exactly.
Everywhere below, 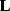 is a binning operator (
is a binning operator (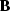 )and
)and 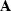 denotes a gradient filter
consisting of two first order derivatives.
denotes a gradient filter
consisting of two first order derivatives.
To suppress the artifacts caused by non-Gaussian noise in the data,
Fomel and Claerbout (1995) introduced a weighting operator W:
| 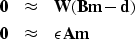 |
|
| (2) |
The choice of the weighting operator 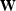 follows two formal principles:
follows two formal principles:
- 1.
- Statistically bad data points (spikes) are indicated by large
values of the residual
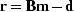
- 2.
- Abnormally large residuals attract most of the conjugate
gradient solvers effort, directing it the wrong way. The
residual should be whitened to distribute the solvers
attention equally among all the data points to emphasize the
role of the ``consistent majority''
Based on these principles operator 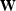 in equation (2)
was chosen by Fomel and Claerbout (1995) to include two components:
the first derivative filter D taken in the space along the
record tracks and the diagonal weighting
operator
in equation (2)
was chosen by Fomel and Claerbout (1995) to include two components:
the first derivative filter D taken in the space along the
record tracks and the diagonal weighting
operator 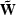 .
.
| 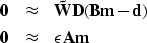 |
|
| (3) |
Fomel and Claerbout (1995) chose weighting function to be 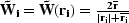 , where
, where
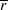 stands for the median of the absolute values from the
whole dataset, and
stands for the median of the absolute values from the
whole dataset, and 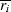 is the median in a small window
around a current point ri.
Since
is the median in a small window
around a current point ri.
Since 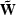 depends upon the residual, the inversion problem
becomes non-linear and system (3) can be solved using a piece-wise linear
approach Fomel and Claerbout (1995). However, Fomel and Claerbout (1995) showed that
while the noisy portion of the model disappeared, the price of the
improvement is a loss of the image resolution.
depends upon the residual, the inversion problem
becomes non-linear and system (3) can be solved using a piece-wise linear
approach Fomel and Claerbout (1995). However, Fomel and Claerbout (1995) showed that
while the noisy portion of the model disappeared, the price of the
improvement is a loss of the image resolution.
In our approach we use a bank of PEFs to decorrelate the residual.
Using Prediction Error Filters as a residual whitener better satisfy the second
of the formal principles used by Fomel and Claerbout (1995). Since
the character of the systematic errors in the data may vary in time
and upon the location of the ship,
an individual PEF 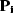 is estimated for
each data track from the residual obtained after solving system
(1). In this case we defined a data track as a series of
measurements recorded with a distance less than 100 meters between
consecutive data points. System (3) then becomes:
is estimated for
each data track from the residual obtained after solving system
(1). In this case we defined a data track as a series of
measurements recorded with a distance less than 100 meters between
consecutive data points. System (3) then becomes:
| 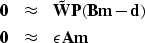 |
|
| (4) |
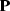 is an operator composed from PEFs
is an operator composed from PEFs 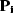 .After a bank of PEFs is estimated we solve this non-linear problem
[equation (4)] in the manner of piece-wise linearization similar to
Fomel and Claerbout (1995). The first step of the piece-wise
linearization is the conventional least squares linearization. The
next step consists of reweighted least squares iterations made in
several cycles with reweighting applied only at the beginning of each
cycle. We chose the weighting function
.After a bank of PEFs is estimated we solve this non-linear problem
[equation (4)] in the manner of piece-wise linearization similar to
Fomel and Claerbout (1995). The first step of the piece-wise
linearization is the conventional least squares linearization. The
next step consists of reweighted least squares iterations made in
several cycles with reweighting applied only at the beginning of each
cycle. We chose the weighting function 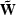 to be
to be 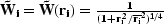 Claerbout (1999).
Claerbout (1999).
In the next section we compare the maps obtained by the three
different methods.





Next: Results
Up: Karpushin and Brown: PEFs
Previous: Data Description
Stanford Exploration Project
9/18/2001
![]() is estimated for
each data track from the residual obtained after solving system
(1). In this case we defined a data track as a series of
measurements recorded with a distance less than 100 meters between
consecutive data points. System (3) then becomes:
is estimated for
each data track from the residual obtained after solving system
(1). In this case we defined a data track as a series of
measurements recorded with a distance less than 100 meters between
consecutive data points. System (3) then becomes: