




Next: Numerical comparisons
Up: Data-space weighting functions
Previous: Data-space weighting functions
With two possible preconditioning operators, 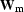 and
and
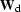 , the question remains, what is the best strategy for
combining them?
, the question remains, what is the best strategy for
combining them?
Chemingui (1999) calculated both 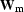 and
and
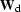 from operator fold and data fold respectively, but
observed that because they both contain the inverse units to the
operator,
from operator fold and data fold respectively, but
observed that because they both contain the inverse units to the
operator, 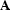 , he should not apply them both at once. Instead he
combined the two preconditioning operators, and solved the system
, he should not apply them both at once. Instead he
combined the two preconditioning operators, and solved the system
| 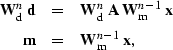 |
(102) |
| (103) |
where 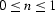 is an adjustable parameter.
Chemingui (1999) provided no advice on the choice of n, but
for the problem he was solving, he observed that applying both
is an adjustable parameter.
Chemingui (1999) provided no advice on the choice of n, but
for the problem he was solving, he observed that applying both
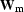 and
and 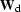 with n=1/2 converged to a
solution more rapidly than either end member (
with n=1/2 converged to a
solution more rapidly than either end member (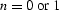 ).
).
The first alternative strategy that I propose is to calculate a
model-space weighting function, 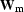 , and use it to
create a new preconditioned system with the form of
, and use it to
create a new preconditioned system with the form of
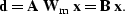
Now probe the composite operator, 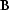 , for a data-space
weighting function for the new system,
, for a data-space
weighting function for the new system,
| 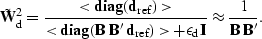 |
(104) |
The new data-space weighting function is dimensionless, and can be
applied in consort with the model-space operator. This leads to a new
system of equations,
| 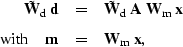 |
(105) |
| (106) |
with appropriate model-space and data-space preconditioning
operators.
The adjoint solution to this system is given by
| 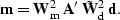 |
(107) |
A second alternative strategy is the corollary of this: create a new
system that is preconditioned by an appropriate data-space weighting
function, and then calculate a model-space weighing function based on
the new system.
The first step is to calculate 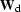 with
equation (
with
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and set up a new system of equations,
), and set up a new system of equations,
| 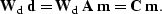 |
(108) |
The second step is to calculate a model-space weighting function based
on this new operator,
| 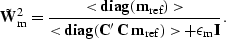 |
(109) |
The preconditioned composite system of equations is now
| 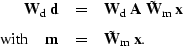 |
(110) |
| (111) |





Next: Numerical comparisons
Up: Data-space weighting functions
Previous: Data-space weighting functions
Stanford Exploration Project
5/27/2001
![]() and
and
![]() from operator fold and data fold respectively, but
observed that because they both contain the inverse units to the
operator,
from operator fold and data fold respectively, but
observed that because they both contain the inverse units to the
operator, ![]() , he should not apply them both at once. Instead he
combined the two preconditioning operators, and solved the system
, he should not apply them both at once. Instead he
combined the two preconditioning operators, and solved the system
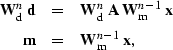
![]() , and use it to
create a new preconditioned system with the form of
, and use it to
create a new preconditioned system with the form of
![]()
![]() with
equation (
with
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and set up a new system of equations,
), and set up a new system of equations,