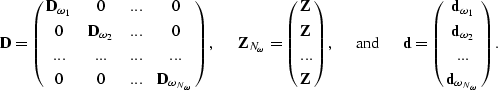| (61) |
| (62) |
| |
(63) | |
| (64) |
If the downward-continuation operator, ![]() , contains
purely a phase-shift, then its adjoint,
, contains
purely a phase-shift, then its adjoint, ![]() will
fully describe the inverse process of upward-continuation.
However, for the amplitudes to be treated accurately,
will
fully describe the inverse process of upward-continuation.
However, for the amplitudes to be treated accurately,
![]() must respect the physics of wave propagation.
Stolt and Benson (1986) show that v(z) extrapolators based on WKBJ
Green's functions contain an amplitude term as well as a phase term,
and for v(x,y,z) earth models this effect is even more pronounced.
So while kinematically-correct extrapolators are
pseudo-unitary, true-amplitude depth extrapolators are not.
In this introductory section, I follow conventional seismic processing
methodology, and treat the depth extrapolator as a unitary operator;
however, in section
must respect the physics of wave propagation.
Stolt and Benson (1986) show that v(z) extrapolators based on WKBJ
Green's functions contain an amplitude term as well as a phase term,
and for v(x,y,z) earth models this effect is even more pronounced.
So while kinematically-correct extrapolators are
pseudo-unitary, true-amplitude depth extrapolators are not.
In this introductory section, I follow conventional seismic processing
methodology, and treat the depth extrapolator as a unitary operator;
however, in section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I discuss how to model
amplitudes correctly.
, I discuss how to model
amplitudes correctly.
The recursion in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be rewritten as:
)
can be rewritten as:
 |
(65) |
| |
(66) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) that can be inverted rapidly by
recursion.
) that can be inverted rapidly by
recursion.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) encapsulates the idea that we can
reconstruct the wavefield at every depth-step in the earth from the
wavefield at the surface by inverting matrix,
) encapsulates the idea that we can
reconstruct the wavefield at every depth-step in the earth from the
wavefield at the surface by inverting matrix, ![]() .
.
As a final step, to produce a migrated image we need to invoke an
imaging condition. For the case of exploding-reflector (zero-offset)
migration [e.g. Claerbout (1995)], we need to extract the image,
![]() , corresponding to t=0.
In the temporal frequency domain, we can do this by summing
over frequency. This stacking process is described by the matrix
equation,
, corresponding to t=0.
In the temporal frequency domain, we can do this by summing
over frequency. This stacking process is described by the matrix
equation,
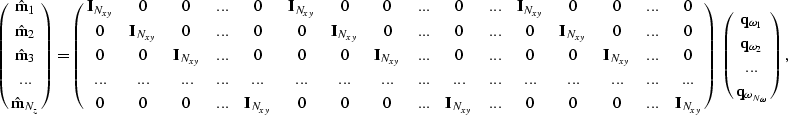
| (67) |
The process of imaging by exploding-reflector migration can then be summarized as the chain of composite operators:
| (68) |